NUMERO DELLE DIAGONALI DI UN POLIGONO
Quante diagonali ha un poligono?
Per rispondere a questa domanda dobbiamo sapere che esiste una formula per conoscere in modo rapido quante diagonali ha un poligono.
Chiamiamo con n il numero di lati del poligono. Ovvero:
n = numero di lati del poligono.
Avremo:
numero diagonali = [n· (n-3)]/ 2.
Ad esempio, vogliamo sapere qual è il numero delle diagonali di un esagono.
Dato che l'esagono ha 6 lati avremo:
n = 6
numero diagonali = [6 · (6-3)]/ 2 =
= (6 · 3)/2 = 18/2 = 9.
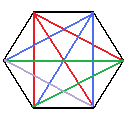
L'esagono ha nove diagonali.
Verifichiamolo provando a disegnare le diagonali dell'esagono:
Vediamo come si può arrivare allo stesso risultato, e a capire anche il senso di questa formula, con un ragionamento.
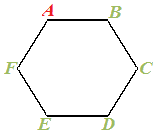
L'esagono ha 6 lati e, quindi, 6 vertici.
Prendiamo uno di questi vertici: il vertice A.
Ora disegniamo tutte le diagonali che partono da A:
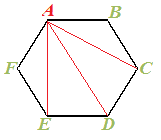
Il vertice A si collega con i restanti vertici tranne i due consecutivi.
Poiché nell'esagono ci sono 6 vertici, il vertice A si collega con altri 3 vertici, ovvero:
6 vertici - se stesso - 2 vertici consecutivi ad A.
Allo stesso modo il vertice B si collega con altri 3 vertici, ovvero:
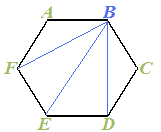
6 vertici - se stesso - 2 vertici consecutivi a B.
Quindi possiamo dire che ogni vertice si collega con i tutti i vertici del poligono, meno se stesso e meno i due consecutivi.
In altre parole ogni vertice si collega con altri (6 - 3) vertici. Quindi da ogni vertice partono 3 diagonali.
Se da un vertice partono 3 diagonali, da 6 vertici partono 18 diagonali ( 6 x 3).
Però teniamo presente che la diagonale che collega, ad esempio, il vertice A al vertice E è la stessa che collega il vertice E al vertice A, quindi devo dividere le 18 diagonali per 2 ottenendo 9 diagonali.
Generalizzando, se ho n vertici, ogni vertice si collega con i restanti, tranne i due consecutivi. Quindi, essendo i vertici n, se ne prendo uno (e dunque considero i restanti n-1) esso si collega con n-3 (cioè n vertici meno se stesso e meno i due vertici consecutivi).
Se da un vertice partono n-3 diagonali, da n vertici partono [n · (n-3)] diagonali.
Tenendo conto che ogni diagonale è stata disegnata due volte, doppiamo dividere il risultato ottenuto per 2.






