DIAGONALI DEL TRAPEZIO ISOSCELE
- Trapezio
- Trapezio isoscele
- Angoli del trapezio isoscele
- Diagonale di un poligono
- Figure geometriche equivalenti e figure geometriche congruenti
- I poligoni
- Implicazione logica
In questa lezione ci occuperemo delle DIAGONALI del TRAPEZIO ISOSCELE.
Ricordiamo che una DIAGONALE di un qualsiasi poligono è ogni SEGMENTO che UNISCE DUE dei suoi VERTICI NON CONSECUTIVI.
Disegniamo il nostro TRAPEZIO ISOSCELE e le sue DIAGONALI:
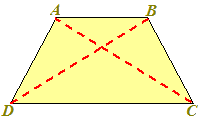
Vogliamo dimostrare che le due diagonali AC e BD sono tra loro CONGRUENTI.
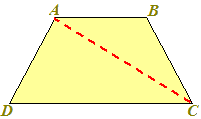
Disegniamo su un cartoncino, il trapezio isoscele ABCD e la diagonale AC:
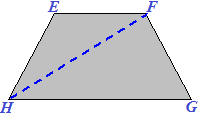
Ora disegniamo su un cartoncino, il trapezio isoscele EFGH e la diagonale FH:
Ritagliamo i due trapezi e li sovrapponiamo ribaltando orizzontalmente il secondo sul primo in modo tale da portare:
- il vertice F sul vertice A;
- il vertice E sul vertice B;
- il vertice G sul vertice D;
- il vertice H sul vertice C.
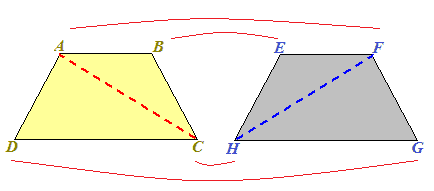
Avremo:
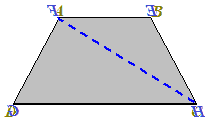
Come possiamo notare le due diagonali coincidono perfettamente, quindi, la diagonale AC del primo trapezio è CONGRUENTE alla diagonale FH del secondo trapezio.
Ma poiché i due trapezi disegnati sono congruenti possiamo dire che la diagonale FH è CONGRUENTE con la diagonale BD, quindi poiché
AC è congruente a FH
e
FH è congruente a BD
avremo che
AC è congruente a BD.
In altre parole:
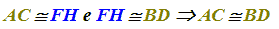
che si legge
se AC è congruente a FH e FH è congruente a BD ciò implica che AC è congruente a BD.






