ARCOCOSENO
Dopo aver parlato, nella lezione precedente, dell'arcoseno, ora andremo a vedere cos'è l'ARCOCOSENO.
Ricordiamo che la FUNZIONE COSENO è:
y = cos α
Sappiamo che il COSENO dell'angolo α può assumere solamente valori compresi tra -1 e 1: questo è il suo CODOMINIO.
Sappiamo, inoltre, che essa è definita per qualsiasi numero reale: l'insieme dei numeri reali R è il suo DOMINIO.
Riportiamo, di seguito, il grafico della funzione coseno dal quale si evincono le caratteristiche appena ricordate:
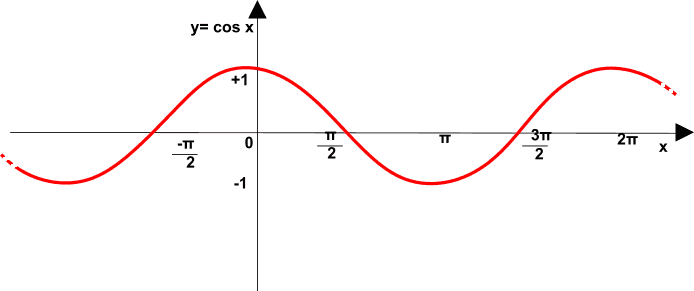
Affinché la funzione coseno sia invertibile è necessario limitare il suo dominio in modo da rendere la funzione biunivoca: andremo, quindi, a considerare l'intervallo 0, π, cioè:
[0, π]
Infatti, andando oltre questo intervallo (sia a destra che a sinistra) accade che, ad uno stesso valore di y, sono associati due valori di x come possiamo vedere, ad esempio, con i punti A e B e con i punti C e D.
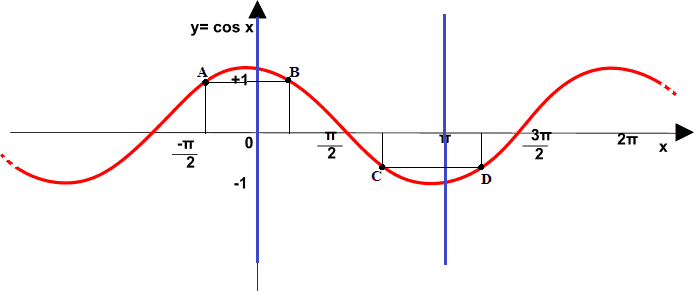
La FUNZIONE INVERSA del COSENO si chiama ARCOCOSENO e si indica con i simboli:
arccos
che si legge
arcocoseno.
o anche con
cos-1
che si legge
coseno alla meno 1.
Supponiamo di avere un angolo, che chiamiamo y il cui coseno vale x, ovvero:
x = cos y
La funzione inversa sarà:
y = arccos x
In altre parole l'ARCOCOSENO è l'ANGOLO che ha un determinato valore di coseno.
Vediamo, adesso, come possiamo costruire il GRAFICO della FUNZIONE ARCOCOSENO.
Iniziamo col prendere il GRAFICO della FUNZIONE COSENO nell'intervallo [0, π]:
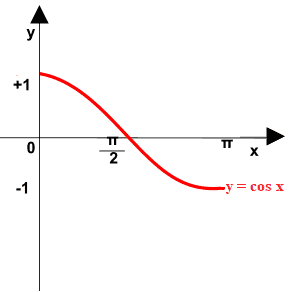
Ora disegniamo la BISETTRICE del PRIMO e del TERZO quadrante, ovvero la retta di equazione
y = x
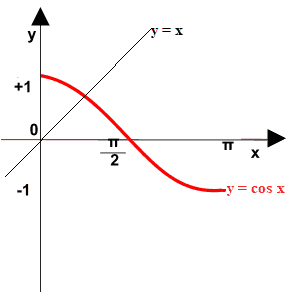
Sullo stesso grafico andiamo a disegnare la curva SIMMETRICA a y = cos x rispetto alla bisettrice del primo e terzo quadrante:

Quello che abbiamo ottenuto è il GRAFICO della FUNZIONE ARCOSENO che riportiamo nell'immagine sottostante dove viene evidenziato come la funzione arcocoseno sia stata ottenuta dalla funzione coseno scambiando i valori della x con quelli della y.
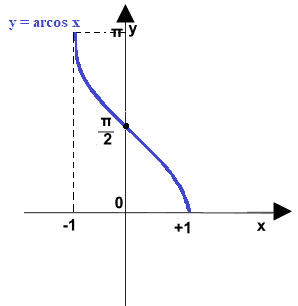
E' evidente, quindi, che la FUNZIONE ARCOCOSENO ha come
DOMINIO: [ -1 , +1 ]
che si legge
intervallo chiuso -1, +1
CODOMINIO: [ 0 , +π ]
che si legge
intervallo chiuso zero, +pi greco






