DIAGONALE DI UN POLIGONO
Consideriamo il POLIGONO ABCDE:

Ora prendiamo il VERTICE B:

Scegliamo un altro VERTICE del poligono, uno qualsiasi, purché NON CONSECUTIVO. Ricordiamo che due vertici si dicono consecutivi quando APPARTENGONO AD UNO STESSO LATO.
Quindi, nel nostro esempio, possiamo scegliere qualsiasi altro vertice ad eccezione di A e C.
Scegliamo, ad esempio, il vertice E:

Quindi disegniamo il SEGMENTO che unisce i PUNTI B ed E:

Quella che abbiamo disegnato si chiama DIAGONALE del poligono.
Ovviamente possiamo fare la stessa cosa con ciascun vertice e i suoi vertici non consecutivi. Allora avremo:

Abbiamo così disegnato tutte le diagonali del nostro poligono. Esse sono:
BE, BD, AC, AD, EC.
Generalizzando possiamo affermare che si dice DIAGONALE di un poligono, ogni SEGMENTO che UNISCE DUE dei suoi VERTICI NON CONSECUTIVI.
Ma quante sono le diagonali di un poligono?
Dipende dal numero di lati, e dunque di vertici, che il poligono ha.
Nel nostro esempio abbiamo un poligono di 5 lati, ovvero un pentagono: esso ha 5 diagonali.
Vediamo di seguito alcuni esempi:
| POLIGONO | DIAGONALI |
|---|---|
| TRIANGOLO:
|
NESSUNA DIAGONALE |
| QUADRILATERO:
|
DUE DIAGONALI |
| PENTAGONO:
|
CINQUE DIAGONALI |
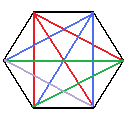
| ESAGONO:
|
NOVE DIAGONALI |
| OTTAGONO:
|
VENTI DIAGONALI |