RECIPROCO DI UN RADICALE
Noi sappiamo che due numeri si dicono RECIPROCI quando il loro PRODOTTO è UGUALE a +1.
Ovvero

Quindi possiamo dire che il reciproco di a è quel numero b tale che moltiplicando il primo per il secondo abbiamo come risultato +1.
La stessa definizione vale anche per i RADICALI.
Quindi possiamo dire che, dato un radicale
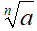
il suo RECIPROCO è
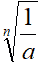
Infatti:
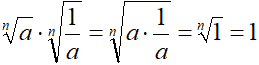
Ovviamente, dobbiamo porre sempre come condizione:
- che a sia MAGGIORE di ZERO se n è PARI, altrimenti il radicale sarebbe privo di significato. Escludiamo il caso in cui a sia uguale a zero perché il denominatore del reciproco sarebbe zero e quindi la frazione sarebbe priva di significato;
- che a sia DIVERSO DA ZERO se n è DISPARI sempre perché altrimenti il denominatore del reciproco sarebbe zero e quindi la frazione sarebbe priva di significato.
Osserviamo, inoltre, che
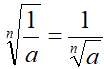
Infatti, studiando il quoziente di due radicali, abbiamo appreso che:
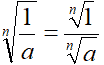
da cui ricaviamo:
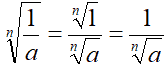
Concludiamo con una precisazione circa il QUOZIENTE di DUE RADICALI aventi lo stesso indice. Ad esempio:
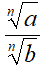
Per dividere un radicale per un altro si può anche MOLTIPLICARE il PRIMO per il RECIPROCO del SECONDO. Infatti, noi sappiamo che il reciproco della radice ennesima di b è:
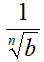
Quindi, possiamo scrivere che
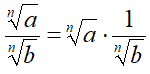
Come possiamo notare i due modi di scrivere si equivalgono: