FIGURE SIMMETRICHE RISPETTO AD UN ASSE
Nella lezione precedente abbiamo introdotto il concetto di
SIMMETRIA ASSIALE.
Ora vedremo come si procede a costruire due figure geometriche simmetriche rispetto ad un asse di simmetria.
Disegniamo una FIGURA PIANA F: nel nostro caso sarà il triangolo ABC
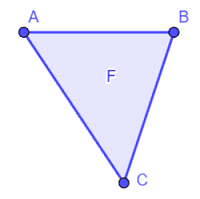
Ora disegniamo la retta r che sarà il nostro ASSE DI SIMMETRIA.

Adesso, procedendo come abbiamo visto nella lezione precedente, costruiamo il punto A' simmetrico del punto A rispetto alla retta r.

Ripetiamo questa costruizione per ognuno dei vertici della figura F in modo da ottenere la figura F'.

F' è il CORRISPONDENTE o TRASFORMATO del triangolo F nella simmetria considerata.
Osserviamo che viene generata una CORRISPONDENZA BIUNIVOCA tra le due figure poiché ad ogni punto della figura F corrisponde un solo punto della figura F' e viceversa.
Ora, su un foglio di carta trasparente, disegniamo la figura F e RIBALTIAMOLA in modo da poterla sovrapporre esattamente alla figura F': noteremo che le due figure sono perfettamente sovrapponibili.
Quindi, possiamo affermare che due figure ottenute per SIMMETRIA ASSIALE sono INVERSAMENTE CONGRUENTI.
Nella prossima lezione continueremo a parlare delle simmetrie assiali e ci soffermermo sul prodotto di due simmetrie assiali.






