CIRCONFERENZE SECANTI
- La circonferenza e il cerchio
- Posizioni reciproche di due circonferenze
- Circonferenze esterne ed interne
- Circonferenze tangenti
- Circonferenze concentriche e corona circolare
- Il piano
- Triangoli
- Caratteristiche dei triangoli
Consideriamo DUE CIRCONFERENZE che chiamiamo C e C' (si legge C primo). Tali circonferenze giacciono sullo STESSO PIANO.
I loro RAGGI sono rispettivamente r e r' (si legge r primo) con
r > r'
si legge
r maggiore di r primo.
Vediamo quando le due circonferenze si dicono SECANTI.
Prima di addentrarci nell'argomento è opportuno ricordare una proprietà dei TRIANGOLI che ci sarà utile in seguito. In un triangolo OGNI LATO è sempre MINORE della SOMMA DEGLI ALTRI DUE e al tempo stesso OGNI LATO è sempre MAGGIORE della DIFFERENZA DEGLI ALTRI DUE.
Ora disegniamo due circonferenze giacenti sullo stesso piano e aventi DUE PUNTI IN COMUNE, il punto A e il punto B:
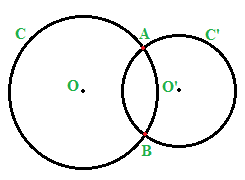
Le due circonferenze disegnate si dicono SECANTI.
Quindi due circonferenze si dicono SECANTI se hanno DUE PUNTI IN COMUNE.
Ora disegniamo:
- la DISTANZA tra i CENTRI delle due circonferenze che indichiamo con OO';
- il raggio OA, della circonferenza C, che chiamiamo r;
- il raggio O'A, della circonferenza C', che chiamiamo r'.
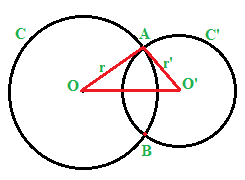
Ora osserviamo il triangolo OO'A: esso ha per lati la distanza tra i centri delle due circonferenze e i due raggi.
Poiché abbiamo detto che in un triangolo ogni lato è sempre minore della somma degli altri due e al tempo stesso è sempre maggiore della differenza degli altri due possiamo scrivere:
OO' < r + r'
e
OO' > r - r'.
Quindi possiamo affermare che due circonferenze sono SECANTI se la DISTANZA dei loro centri è:
- MINORE della SOMMA dei loro RAGGI
e
- MAGGIORE della loro DIFFERENZA.
Nelle prossime lezioni esamineremo le altre posizioni reciproche che possono avere due circonferenze.






