FORMULE GONIOMETRICHE
Parlando degli ANGOLI NOTEVOLI abbiamo visto i valori assunti dai principali angoli.
Per introdurre il tema delle FORMULE GONIOMETRICHE soffermiamoci a considerare gli angoli di 30° e di 60°.
Il seno dell'angolo di 30° è pari ad 1/2, mentre il seno dell'angolo di 60° è pari a √3/2.
Quindi possiamo scrivere:

e

Noi possiamo dire che:
60° = 2 · 30°
Questo potrebbe indurci a pensare che il seno dell'angolo di 60° (cioè 2 · 30°) sia uguale a due volte il seno dell'angolo di 30°. Verifichiamo se ciò è vero:


Quindi possiamo vedere chiaramente che il seno dell'angolo di 60° (cioè 2 · 30°) non è uguale al doppio del seno di 30°:

che si legge:
il seno dell'angolo di 30° è diverso dal doppio del seno dell'angolo di 30°.
Generalizzando, se poniamo:
α = 30°
si avrà che:
2 · α = 60°
pertanto potremo scrivere che:
sen (2α) ≠2 sen α
che si legge:
il seno dell'angolo due volte alfa è diverso dal doppio del seno dell'angolo alfa.
Cosa significa questo? Che se il valore di un angolo diventa doppio (ma vale anche per il triplo, il quadrulplo e così via, come si può facilmente verificare), il valore della funzione seno non diventa anch'essa doppia o tripla.
Questo vuol dire che la funzione SENO NON varia in MANIERA PROPORZIONALE al variare dell'angolo.
Questa considerazione non riguarda solamente il seno di un angolo, ma tutte le funzioni goniometriche: lasciamo a voi la dimostrazione che, come si è potuto notare, è estremamente semplice.
Quindi possiamo affermare che le FUNZIONI GONIOMETRICHE variano al variare dell’angolo α, ma NON variano in maniera PROPORZIONALE ad esso.
Facciamo ora un'altra considerazione in merito alle funzioni goniometriche.
Consideriamo il seno dell'angolo di 30°, 90° e 120°.
Sappiamo che


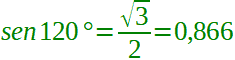
Possiamo osservare che:
120° = 90° + 30°
Quindi possiamo scrivere che:
sen 120° = sen (90° + 30°)
Ma come possiamo facilmente notare il seno dell'angolo di 120° non è uguale alla somma del seno dell'angolo di 90° e del seno dell'angolo di 30°. Infatti:
sen (90° + 30°) = 0,866
mentre
sen 90° + sen 30° = 1 + 0,5 = 1,5
Quindi possiamo dire che:
sen (90° + 30°) ≠ sen 90° + sen 30°
Ragioniamo in maniera simile per ciò che concerne la sottrazione. Possiamo dire che:
90° = 120° - 30°
Da cui otteniamo:
sen 90° = sen (120° - 30°)
Ma come possiamo facilmente notare il seno dell'angolo di 90° non è uguale alla differenza del seno dell'angolo di 120° e del seno dell'angolo di 30°. Infatti:
sen (120° - 30°) = 1
mentre
sen 120° - sen 30° = 0,866 - 0,5 = 0,366
Quindi possiamo dire che:
sen (120° - 30°) ≠ sen 120° - sen 30°
Generalizzando possiamo scrivere che:
sen (α + β) ≠ sen α + sen β
che si legge:
il seno dell'angolo, alfa più beta, è diverso dal seno dell'angolo alfa più il seno dell'angolo beta
come pure possiamo dire che:
sen (α - β) ≠ sen α - sen β
che si legge:
il seno dell'angolo, alfa meno beta, è diverso dal seno dell'angolo alfa meno il seno dell'angolo beta.
Il discorso sin qui fatto non è valido solamente nel caso del seno di un angolo, ma anche per tutte le altre funzioni goniometriche (coseno, tangente, cotangente).
Come fare, allora, per calcolare la funzione goniometrica della somma o della differenza di due angoli? Come calcolare la funzione goniometrica del doppio o del triplo di un dato angolo? Come calcolare la funzione goniometrica della metà di un certo angolo?
In nostro aiuto vengono alcune formule che prendono il nome di FORMULE GONIOMETRICHE.
Nelle prossime lezioni vedremo meglio di cosa si tratta e quali sono queste formule.






