SIGNIFICATO GONIOMETRICO DEL COEFFICIENTE ANGOLARE DI UNA RETTA
In questa lezione concluderemo l'argomento relativo alle funzioni goniometriche occupandoci del SIGNIFICATO GONIOMETRICO del COEFFICIENTE ANGOLARE di una RETTA.
Disegniamo una CIRCONFERENZA GONIOMETRICA.
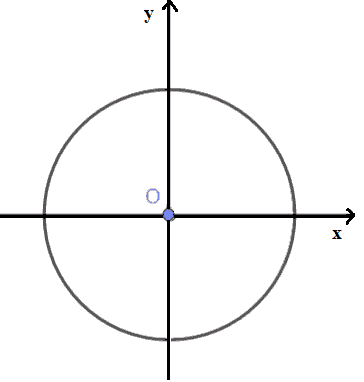
e disegniamo una RETTA PASSANTE PER L'ORIGINE DEGLI ASSI la cui equazione è:
y = mx
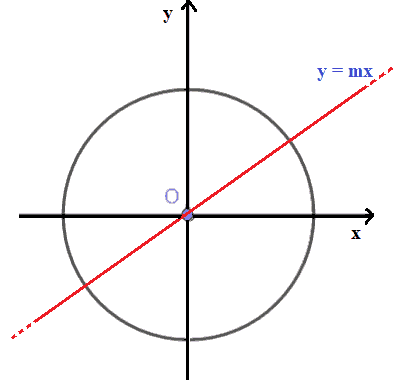
Chiamiamo α l'angolo orientato formato dalla retta, che abbiamo appena disegnato, con l'asse delle x.
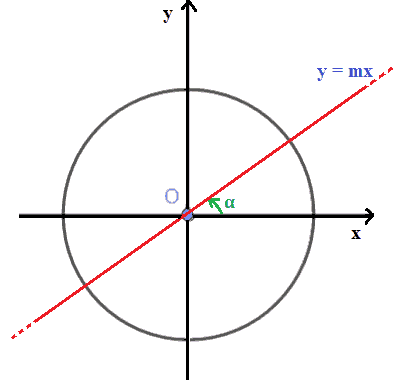
Dall'equazione della retta andiamo a ricavarci il valore di m dividendo entrambi i membri dell'equazione per x . Chiaramente per fare questo dobbiamo porre come condizione che
x ≠ 0
e avremo:
y/x = (mx)/x
m = y/x
Ora disegniamo il punto A della circonferenza goniometrica di coordinate:
A (1 ; 0)
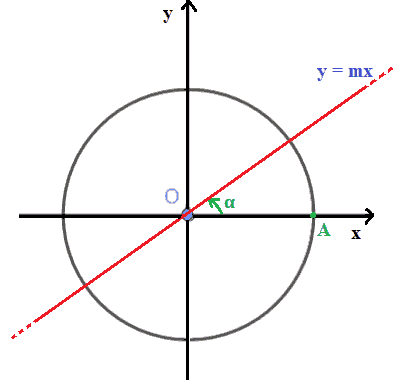
e disegniamo la retta tangente alla circonferenza goniometrica nel punto A
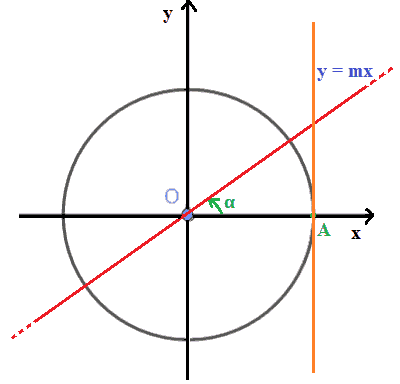
Indichiamo con T il punto di intercessione della retta passante per l'origine degli assi e della retta AT: sappiamo che l'ordinata del punto T è la tangente dell'angolo α.

Sappiamo, però, che la tangente è anche il rapporto tra il segmento AT e il segmento OA.
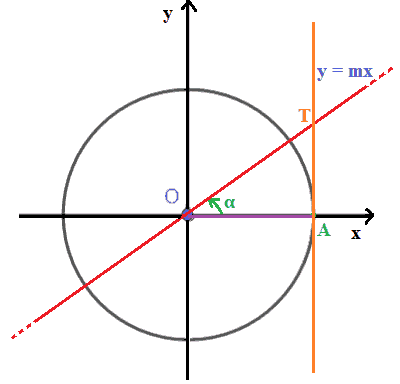
Ma il segmento AT non è altro che l'ordinata del punto T, mentre il segmento OA non è altro che l'ascissa del punto A e quest'ultima sappiamo che è 1.
Quindi possiamo scrivere:
tan α = yT /1 = yT
Chiaramente, fermo restanto che il punto T è il punto di intersezione tra una qualsiasi retta passante per l'origine degli assi e la retta che interseca la circonferenza goniometrica nel punto di A, possiamo generalizzare e scrivere:
tan α = y
Abbiamo visto, poc'anzi, che
m = y/ x
Ma se
y = tan α e x = 1
il coefficiente angolare m diventa:
m = tan α / 1 = tan α
Quindi possiamo affermare che il COEFFICIENTE ANGOLARE della retta è UGUALE alla TANGENTE dell’angolo formato tra la retta stessa e l’asse x.
Fin qui abbiamo parlato di rette passanti per l'origine degli assi. Ora vogliamo generalizzare il discorso a tutte le rette.
Abbiamo detto che il coefficiente angolare di una retta passante per l'orgine degli assi è uguale alla tangente dell’angolo che la retta forma con l’asse x.
Disegniamo gli assi cartesiani e la retta r passante per l'origine degli assi e avente come equazione:
y = mx
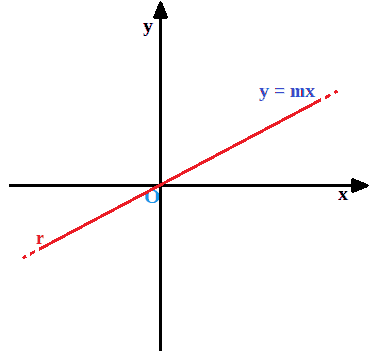
Ora andiamo a disegnare una seconda retta, che chiamiamo r', PARALLELA ad r:
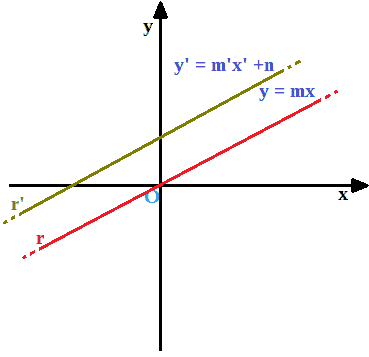
Chiaramente la retta r' non passa per l'origine degli assi e, quindi, la sua equazione sarà:
y' = m'x' + n'
Ma noi sappiamo, dallo studio della geometria analitica, che due rette sono parallele quando hanno lo STESSO COEFFICIENTE ANGOLARE, questo significa che
m = m'
Ora chiamiamo con α l'angolo formato dalla retta r con l'asse delle x e con α' l'angolo formato dalla retta r' con l'asse delle x:
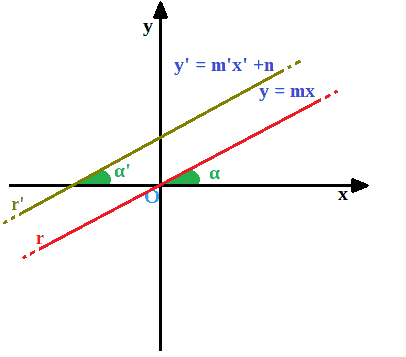
Due RETTE PARALLELE formano con l'asse delle x due ANGOLI CONGRUENTI. Quindi
α ≅ α'
che si legge
alfa congruo ad alfa primo.
Quindi possiamo dire che
m' = tan α'
Questo ci permette di estendere le conclusioni alle quali eravamo giunti, nel caso di rette passanti per l'origine degli assi, anche alle rette che non passano per l'origine degli assi.
Di conseguenza possiamo affermare che vale sempre la regola in base alla quale il COEFFICIENTE ANGOLARE della retta è UGUALE alla TANGENTE dell’angolo formato tra la retta stessa e l’asse delle x.






