DISTANZA TRA DUE PUNTI: ESERCIZI
- Assi cartesiani ortogonali
- Rappresentazione di un punto su un pianto cartesiano
- Rappresentazione di un punto su un pianto cartesiano: alcuni esempi
- Rappresentazione di un punto su un pianto cartesiano: casi particolari
- Distanza tra due punti aventi la stessa ordinata
- Distanza tra due punti aventi la stessa ascissa
- Distanza tra due punti sul piano
- Distanza tra due punti sul piano cartesiano
- Triangoli
- Perimetro del triangolo
- Il segmento
- Area del triangolo
Nelle lezioni precedenti abbiamo visto come calcolare la DISTANZA TRA DUE PUNTI sul piano cartesiano. In questa lezione vedremo, come applicare le nozioni apprese risolvendo un esercizio.
Esercizio:
i punti A (6; 9), B (3/2; 3), C (4;9) sono i vertici di un triangolo. Determinare il perimetro e l'area del triangolo ABC.
Iniziamo col rappresentare i tre punti sugli assi cartesiani:
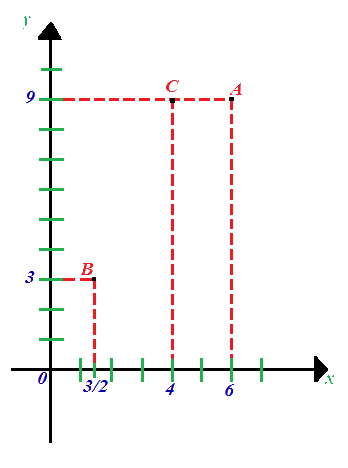
Ora congiungiamo i tre punti e disegniamo il nostro triangolo:
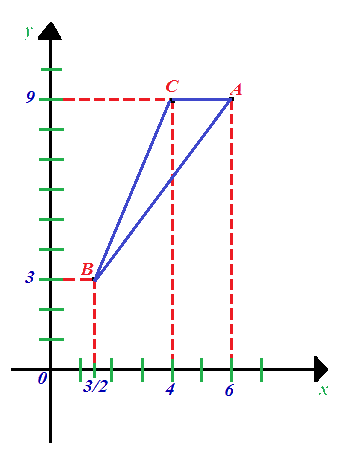
Ora dobbiamo trovare il perimetro del nostro triangolo. Per fare ciò dobbiamo calcolare la misura dei tre segmenti BA, AC, CB: si tratterà di applicare le formule che abbiamo appreso nelle lezioni precedenti sulla distanza tra due punti.
Iniziamo dal segmento BA:

Passiamo al segmento AC:
AC = |4 - 6| = |-2| = 2.
Infine troviamo la misura del segmento CB:

Ed ora possiamo trovare il perimetro cercato. Esso è dato dalla somma dei tre segmenti, ovvero:
P = 15/2 + 2 + 13/2 =
= (15 + 4 + 13)/ 2 = 32/2 = 16.
Ora passiamo a calcolare l'AREA DEL TRIANGOLO. Essa si ottiene moltiplicando la base per l'altezza e dividendo il prodotto per 2.
Scegliamo come base del triangolo il segmento AC e tracciamo la relativa altezza, ovvero il segmento BH:
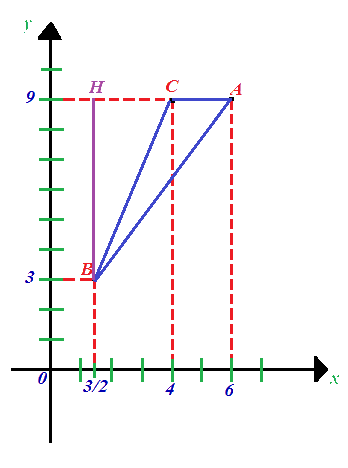
Ora noi sappiamo che:
- il segmento AC, cioè la base del triangolo, misura 2;
- sappiamo che il punto B ha coordinate 3/2 e 3;
- e possiamo vedere che il punto H ha coordinate 3/2 e 9.
Quindi possiamo trovare la misura del segmento BH, ovvero l'altezza del triangolo. Avremo:
BH = |9 - 3| = |6| = 6.
Quindi l'area del triangolo si ottiene facendo:
A = (b x h)/ 2 = (2 x 6)/ 2 = 12/ 2 = 6.






