EQUAZIONE DELLA RETTA TANGENTE ALLA CIRCONFERENZA E PASSANTE PER UN PUNTO P
- Equazione della circonferenza
- Posizione di una retta rispetto ad una circonferenza
- Equazione della retta tangente alla circonferenza e passante per un punto P
- Equazione della retta tangente alla circonferenza e passante per un punto P appartenente alla circonferenza
- Formule di sdoppiamento nella circonferenza
Nelle lezioni precedenti abbiamo visto come possiamo scrivere l'equazione della retta tangente alla circonferenza per un punto P appartenente alla circonferenza stessa.
Ora vedremo come possiamo trovare l'equazione della RETTA TANGENTE alla CIRCONFERENZA e passante per un punto P, quando:
- P NON APPARTIENE alla circonferenza;
- non sappiamo se P appartiene o meno alla circonferenza.
Anche in questi casi si possono usare due metodi diversi: in questa lezione vedremo il primo di questi metodi, mentre nella prossima lezione vedremo il secondo.
Per risolvere questo tipo di problema occorre:
- scrivere il FASCIO
di RETTE passante per P.
Ricordiamo che la formula è
y - y0 = m (x - x0).
Da essa ci dobbiamo ricavare il valore di y:
y = mx - mx 0 + y
-
mettere a SISTEMA
l'equazione della CIRCONFERENZA
con quella del FASCIO di RETTE
passante per P;
- SOSTITUIRE,
nell'equazione
della circonferenza, alla y
il valore
mx - mx0 + y;
- porre la CONDIZIONE di TANGENZA,
Δ = 0.
Infatti se il discriminante fosse minore di zero, la retta sarebbe esterna rispetto alla circonferenza, mentre se il discriminante fosse maggiore di zero, la retta sarebbe secante alla circonferenza;
- cercare il valore del COEFFICIENTE
ANGOLARE. Troveremo:
- DUE valori distinti se il punto P è ESTERNO alla circonferenza;
- UN SOLO valore se il punto P APPARTIENE alla circonferenza;
- SOSTITUIRE il valore del coefficiente angolare nell'equazione del FASCIO di rette e trovare la retta tangente alla circonferenza. Chiaramente, se abbiamo trovato due coefficienti angolari, avremo due rette tangenti alla circonferenza, se ne abbiamo trovato uno solo avremo una sola retta tangente alla circonferenza.
Esempio:
scrivere l'equazione della retta tangente alla circonferenza di equazione x2 + y2 - 9 = 0 passante per il punto P(5; 0).
Iniziamo scrivendo il fascio di rette passante per il punto P:
y - y0 = m (x - x0)
y - 0 = m(x - 5)
y = mx - 5m.
Mettiamo a sistema l'equazione della circonferenza con l'equazione del fascio di rette:
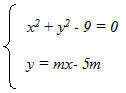
Nella prima equazione, dove troviamo il valore y, sostituiamo con
mx - 5m.
x2 + y2 - 9 = 0
x2 + (mx - 5m)2 - 9 = 0
x2 + m2x2 + 25m2 - 10m2x - 9 = 0
(1 + m2) x2 - 10m2x + 25m2 - 9 = 0.
Osserviamo che
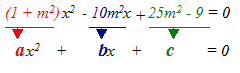
Poniamo la condizione di tangenza e troviamo il valore di m:
Δ = 0
Δ = b2 - 4ac = 0
100m4 - 4 · (1 + m2) · (25m2 - 9) = 0
100m4 + (-4 - 4m2) · (25m2 - 9) = 0
100m4 - 100m2 + 36 - 100m4 + 36m2 = 0.
Sommiamo i termini simili:
- 64m2 + 36 = 0.
Da cui abbiamo
- 64m2= -36
64m2 = 36
m2 = 36/64
m2= 9/16
m = ±3/4.
Abbiamo ottenuto due risultati. Questo significa che il punto P è esterno alla circonferenza e ci sono due rette tangenti alla circonferenza e passanti per tale punto. Le equazioni delle tangenti le otteniamo sostituendo, nell'equazione del fascio di rette passanti per P, i due coefficienti angolari trovati. Ovvero:
y = mx - 5m.
Quindi la prima tangente ha come equazione:
y = -3/4x -5 ·(-3/4)
y = -3/4x + 15/4.
Mentre la seconda tangente ha come equazione:
y = 3/4x -5 ·(3/4)
y = 3/4x - 15/4.
Facciamo ora una precisazione. Questo metodo può portare, spesso, a dover risolvere calcoli molto complessi. Nell'esempio da noi scelto, infatti, abbiamo semplificato usando una circonferenza con centro nell'origine degli assi (a = 0 e b = 0). Inoltre, il punto per il quale passano le rette tangenti ha come ordinata 0. Di fronte a casi diversi da questo, i conteggi possono risultare molto lunghi e può essere facile cadere in errore. Per questo può risultare preferibile usare il metodo che illustreremo nella prossima lezione.






