EQUAZIONE DELLA RETTA TANGENTE ALLA CIRCONFERENZA E PASSANTE PER UN PUNTO P

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Equazione della circonferenza
• Posizione di una retta rispetto ad una circonferenza
• Equazione della retta tangente alla circonferenza e passante per un punto P
• Equazione della retta tangente alla circonferenza e passante per un punto P appartenente alla circonferenza
• Formule di sdoppiamento nella circonferenza
• Equazione della retta tangente alla circonferenza e passante per un punto P
• Equazione della circonferenza: casi particolari
• Distanza di un punto da una retta: forma esplicita

Passiamo a vedere il secondo metodo che possiamo usare per trovare l'equazione della RETTA TANGENTE alla CIRCONFERENZA e passante per un punto P.

Per comprendere tale metodo, facciamo una premessa.

Disegniamo una circonferenza e le rette tangenti ad essa e passanti per un punto P esterno alla circonferenza (lo stesso discorso si può fare anche se il punto P appartiene alla circonferenza).

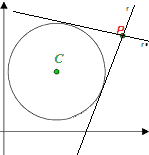
Ora osserviamo che, la DISTANZA tra il CENTRO della circonferenza e la TANGENTE r, non è altro che il RAGGIO.

Allo stesso modo la distanza tra il centro della circonferenza e la tangente r', è ancora una volta il RAGGI.

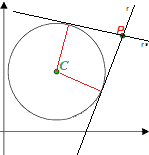
Allora procediamo nel modo seguente:

• scriviamo il FASCIO di RETTE passante per P. La formula da applicare è

  y - y₀ = m (x - x₀)

  
  
  
• calcoliamo le coordinate del CENTRO e il RAGGIO della circonferenza. Ricordiamo che

  -2α = a

  -2β = b

  α² +β² - r² = c
  
  

• calcoliamo la DISTANZA tra il centro della circonferenza C e il FASCIO di RETTE passante per P. Utilizziamo la forma esplicita della formula della distanza di un punto da una retta:

  
  
  

  
  
  
• troviamo il valore di m. Avremo una sola soluzione se il punto P appartiene alla circonferenza. Troveremo, invece, due valori se il punto P è esterno alla circonferenza
  
  
• SOSTITUIAMO il valore del coefficiente angolare nell'equazione del FASCIO di rette e avremo la retta tangente alla circonferenza. Chiaramente, se abbiamo trovato due coefficienti angolari, avremo due rette tangenti alla circonferenza, se ne abbiamo trovato uno solo avremo una sola retta tangente alla circonferenza.

Riprendiamo l'esercizio visto nella lezione precedente e vediamo come avremmo potuto risolverlo applicando tale metodo.

Esempio:

scrivere l'equazione della retta tangente alla circonferenza di equazione x² + y² - 9 = 0 passante per il punto P(5; 0).

Partiamo dal fascio di rette passante per il punto P:

y - y₀ = m (x - x₀)

y - 0 = m(x - 5)

y = mx - 5m.

Ora cerchiamo le coordinate del centro e il raggio della circonferenza.

-2α = a

-2α = 0

α = 0.

-2β = b

-2β = 0

β = 0.

Quindi

C (0; 0).

Che il centro fosse nell'origine degli assi era comunque evidente dalla stessa equazione della circonferenza.

Andiamo a cercare il raggio:

α² +β² - r² = c

0 +0 - r² = c

- r² = - 9

r² = 9

r = 3.

Scriviamo la distanza tra il centro C della circonferenza e il fascio di rette passante per P e la poniamo pari al raggio r:

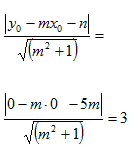
Risolviamo in modo da trovare il valore di m:

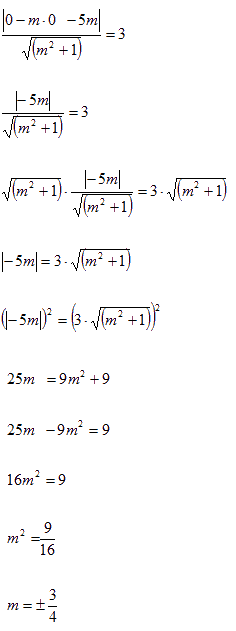
Poiché abbiamo trovato due risultati possiamo dire che il punto P è esterno alla circonferenza e, di conseguenza, avremo due rette tangenti alla circonferenza passanti per il punto P. Le equazioni delle tangenti le otteniamo sostituendo, nell'equazione del fascio di rette passanti per P, i due coefficienti angolari trovati. Ovvero:

y = mx - 5m.

Quindi la prima tangente ha come equazione:

y = -3/4x -5 ·(-3/4)

y = -3/4x + 15/4.

Mentre la seconda tangente ha come equazione:

y = 3/4x -5 ·(3/4)

y = 3/4x - 15/4.

Come possiamo notare abbiamo ottenuto gli stessi risultati visti nella lezione precedente.

Lezione precedente - Lezione successiva

Indice argomenti su equazione della circonferenza

Pubblicità/Advertising