FORMULE DI PROSTAFERESI PER LA TANGENTE
- Seconda relazione fondamentale della goniometria
- Formula di addizione del seno
- Formula di sottrazione del seno
Dopo aver visto le formule di prostaferesi per il seno e per il coseno, in questa lezione ci occuperemo delle FORMULE DI PROSTAFERESI per la TANGENTE.
Queste si ricavano usando le relazioni fondamentali della goniometria e le formule di addizione e sottrazione del seno.
Dalla SECONDA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA sappiamo che la TANGENTE di un angolo può essere scritta come il RAPPORTO tra il SENO e il COSENO dello stesso angolo.
Di conseguenza
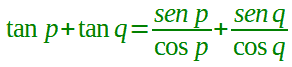
Eseguiamo i calcoli:
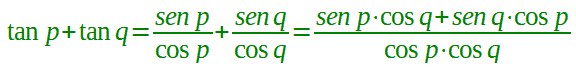
Osserviamo il numeratore della frazione e ricordiamo che la FORMULA DI ADDIZIONE del SENO ci dice che:
sen (α + β) = sen α · cos β + cos α · sen β
Quindi, il nostro numeratore non è altro che il SENO della somma di p + q.
Di conseguenza la nostra formula diventa:

Chiaramente dobbiamo porre come condizione che il denominatore della frazione sia diverso da zero. In altre parole è necessario porre la condizione:
cos p · cos q ≠ 0
che equivale a dire
cos p ≠ 0
e
cos q ≠ 0
Ora noi sappiamo che il coseno di un angolo è uguale a 0 quando l'angolo misura 90°, 270° e così via. Quindi, la condizione da porre sarà:
p ≠ π/2 + kπ
e
q ≠ π/2 + kπ
con k ∈ Z
Passiamo ad esaminare la formula:
tan p - tan q
che, per quanto detto prima, possiamo scrivere nel modo seguente:
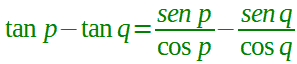
Eseguiamo i calcoli:
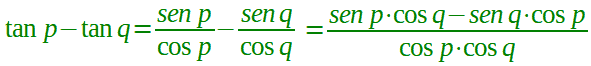
Osserviamo il numeratore della frazione e ricordiamo che la FORMULA DI SOTTRAZIONE del SENO ci dice che:
sen (α - β) = sen α · cos β - cos α · sen β
Quindi, il nostro numeratore non è altro che il SENO della differenza di p - q.
Di conseguenza la nostra formula diventa:

Chiaramente anche in questo caso dobbiamo porre come condizione che il denominatore della frazione sia diverso da zero. E, come abbiamo visto nella formula precedente, questo accade quando
p ≠ π/2 + kπ
e
q ≠ π/2 + kπ
con k ∈ Z
Nella prossima lezione vedremo le formule di prostaferersi per la cotangente.






