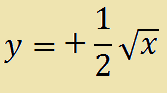FUNZIONE INVERSA DI UNA PARABOLA
- Funzioni inverse
- Come trovare la funzione inversa di una funzione?
- Esempi di calcolo di una funzione inversa
- Funzione inversa di una funzione logaritmica
- Funzione invertibile in un intervallo
- Funzione invertibile e monotona
- Funzioni iniettive
- Come riconoscere se una funzione è iniettiva
- Come capire se una funzione è iniettiva
- Funzioni suriettive
- Come riconoscere se una funzione è suriettiva
- Funzioni biunivoche
- Come riconoscere se una funzione è biunivoca
- Assi cartesiani ortogonali
- Parabola
Consideriamo la funzione
y = 4x2.
La funzione data è la funzione di una PARABOLA avente il vertice nell'origine degli assi cartesiani:
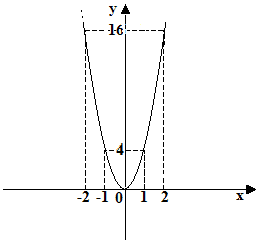
Questa funzione NON è INIETTIVA, poiché ad elementi diversi di X non corrispondono elementi diversi di Y.
Esempio:
quando x = 1, y= 4
quando x = - 1, y = 4.
Di conseguenza la funzione sicuramente NON E' INVERTIBILE.
Tuttavia, se facciamo delle RESTRIZIONI diventa possibile calcolarne la FUNZIONE INVERSA.
Ad esempio, se consideriamo il vertice e metà della parabola la funzione diventa iniettiva.
Tale funzione è anche suriettiva poiché ogni elementi di Y è immagine di almeno un elemento di Y.
Quindi, restringendo il dominio della funzione in modo da considerare solamente il vertice e metà della parabola,, la funzione diventa invertibile. Consideriamo, allora, la parte del grafico evidenziata in giallo:

Ora determiniamo la funzione inversa scambiando, nella funzione f, la x con la y.
Partiamo dalla funzione f e avremo:
y = 4x2
x = 4y2.
Da cui possiamo scrivere:
4y2 = x.
Dividiamo primo e secondo membro per 4:
(4y2)/4 = x/4
y2 = x/4.
Estraiamo la radice da entrambi i membri e otteniamo:
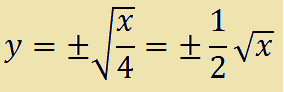
Poiché abbiamo considerato solamente metà del grafico, la metà positiva, considereremo funzione inversa solamente il radicale positivo. Ovvero: