EQUAZIONE DELLA PARABOLA
- Parabola
- Parabola con vertice nell'origine degli assi
- Equazione della parabola con asse di simmetria parallelo all'asse delle y
- Distanza tra due punti sul piano cartesiano
- Raccoglimento a fattor comune
Nella lezione precedente abbiamo visto che
y = ax2 + bx + c
è l'equazione di una PARABOLA con ASSE DI SIMMETRIA PARALLELO all'ASSE delle y.
Il VERTICE di tale parabola ha come coordinate:
V ( -b/2a ; -Δ/ 4a).
L'ASSE DI SIMMETRIA della parabola è la retta di equazione:
x = -b/2a.
Vediamo ora come si definisce la parabola.
La PARABOLA è il luogo geometrico dei PUNTI del piano EQUIDISTANTI da un PUNTO FISSO detto FUOCO e da una RETTA FISSA della DIRETTRICE.

Il FUOCO:
- NON APPARTIENE mai alla parabola;
- NON E' mai ESTERNO alla parabola.
Supponiamo che il fuoco abbia coordinate:
F (p ; q).
La direttrice abbiamo ipotizzato che abbia equazione:
y = d.
Poiché, per definizione, ogni punto P (x; y) della parabola è equidistante dal fuoco e dalla direttrice, possiamo scrivere che:

Applicando le formule della distanza tra due punti possiamo scrivere:
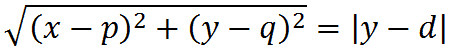
Eleviamo primo e secondo membro al quadrato ed otteniamo:
(x - p)2 + (y - q)2 = (y - d)2.
Sviluppiamo i quadrati:
x2 + p2 -2px + y2 + q2 - 2qy = y2 + d2 - 2dy.
Togliamo, a primo e secondo membro, y2:
x2 + p2 -2px + y2 + q2 - 2qy = y2 + d2 - 2dy
x2 + p2 -2px + q2 - 2qy = d2 - 2dy.
Portiamo, a primo membro, tutti i termini contenenti la y, cambiando di segno e portiamo a secondo membro tutti gli altri termini, cambiando di segno:
x2 + p2 -2px + q2 - 2qy = d2 - 2dy
- 2qy + 2dy = d2 - x2 - p2 +2px - q2.
Moltiplichiamo, entrambi i termini, per -1:
+ 2qy - 2dy = - d2 + x2 + p2 - 2px + q2.
A primo membro mettiamo in evidenza 2y:
2y (q - d) = - d2 + x2 + p2 - 2px + q2.
A secondo membro raccogliamo insieme i termini noti (cioè quelli che non contengono la x):
2y (q - d) = x2 - 2px + (q2 - d2 + p2).
Dividiamo entrambi i membri per 2(q - d):

Da cui ricaviamo che:


E poniamo:
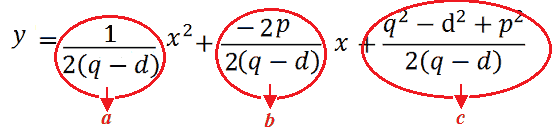
Avremo:
y = ax2 + bx + c.
Abbiamo così ottenuto l'EQUAZIONE DELLA PARABOLA.
Nella prossima lezione esamineremo meglio fuoco e direttrice.






