TRASPORTO DI UN FATTORE FUORI DAL SIMBOLO DI RADICE
- Radicali di indice n
- Trasporto di un fattore fuori dal simbolo della radice
- Trasporto di un fattore fuori dal simbolo della radice
- Trasporto di un fattore fuori dal simbolo della radice
- Proprietà delle potenze
- Prodotto tra radicali
- Seconda proprietà fondamentale dei radicali
Continuiamo a parlare del TRASPORTO di un fattore FUORI del simbolo di RADICE, ed esaminiamo l'ultimo caso, ovvero quello nel quale, nel radicando, compare una POTENZA con ESPONENTE che NON è MULTIPLO dell'INDICE della radice.
Anche in questo caso, così come abbiamo fatto nella lezione precedente, per semplicità ci limiteremo a considerare il caso in cui il fattore a sia positivo.
Esempio:

Ora, poiché abbiamo detto che m non è multiplo di n, significa che se dividiamo m per n otterremo un resto r diverso da zero. In altre parole
m = n· q + r
con
r ≠ 0.
Quindi possiamo dire che:
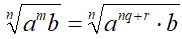
Ma noi sappiamo che il prodotto di due o più potenze aventi la stessa base è una potenza della stessa base con esponente uguale alla somma degli esponenti. Quindi possiamo scrivere:
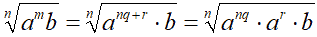
Ora applichiamo la proprietà della potenza di una potenza e scriviamo:
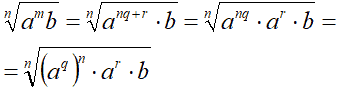
Da quanto abbiamo appreso circa il trasporto di un fattore fuori del simbolo di radice, nel caso in cui l'esponente del fattore è uguale all'indice della radice, possiamo scrivere:
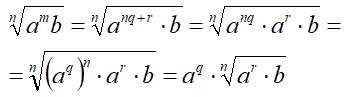
Quindi ne deduciamo che
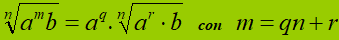
che si legge
radice ennesima di a elevato ad m per b
è uguale
ad a elevato a q per la radice ennesima di a elevato ad r per b
con
m uguale a q per n più r.
Vediamo qualche esempio:







