PRODOTTO DI DUE ROTAZIONI
Nelle lezioni precedenti abbiamo visto come si procede ad effettuare la ROTAZIONE di una FIGURA PIANA.
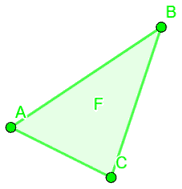
Supponiamo, ora, di avere una FIGURA PIANA che chiameremo F: nel nostro caso sarà un triangolo.
Ora costruiamo il suo trasformato F' rispetto ad una ROTAZIONE R di centro O, di ampiezza β (che si legge beta), e di un dato verso (nel nostro grafico il verso è orario).

Adesso costruiamo il trasformato di F' rispetto ad una ROTAZIONE R' SEMPRE di centro O, ma di ampiezza γ (che si legge gamma), e dello STESSO VERSO (quindi, nel nostro grafico sempre di verso orario) e lo chiameremo F'' .
ATTENZIONE quindi!!!!CENTRO e VERSO della rotazione devono essere gli STESSI, mentre l'ampiezza può essere diversa.

In questi casi si dice che il triangolo F è stato trasformato nel triangolo F'' mediante il PRODOTTO delle delle due ROTAZIONI R ed R'.
E' evidente che, partendo dalla figura F, avremmo potuto ottenere direttamente la figura F'' mediante una rotazione di centro O, e di ampiezza pari a β + γ e di verso orario.
Per non appesantire l'immagine sottostante e renderla più chiara abbiamo evidenziato solamente le rotazioni R ed R' del punto A del triangolo.

Per concludere possiamo dire che il PRODOTTO di due ROTAZIONI di centro O e anch'esso una ROTAZIONE di centro O.






