SECONDA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA
Nella lezione precedente abbiamo appreso che la TANGENTE di un angolo orientato α è l'ORDINATA del punto in cui, la RETTA TANGENTE alla circonferenza goniometrica nel suo punto di ascissa 1, incontra la retta OP, dove P è il punto associato all'angolo α.
Ovvero:
T (1; tan α)
In questa lezione vedremo un'altra definizione di tangente.
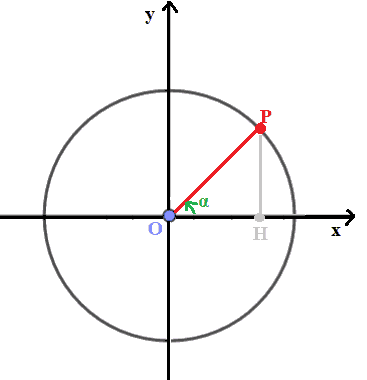
Disegniamo la circonferenza goniometriaca e l'angolo orientato α

Ora andiamo a disegnare due TRIANGOLI aventi IN COMUNE l'ANGOLO ACUTO α:
- il triangolo OHP
- il triangolo OAT
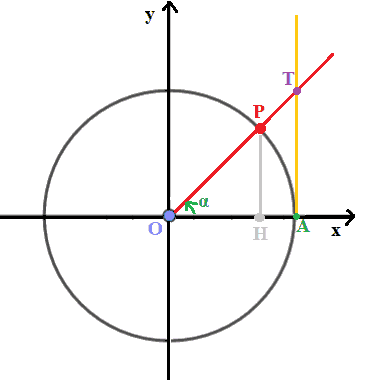
I due TRIANGOLI da noi disegnati sono due triangoli rettangoli, infatti, sia la retta PH che la retta TA sono perpendicolari all'asse delle ascisse e, quindi, formano con essa quattro angoli retti.
Noi sappiamo che, quando due triangoli rettangoli hanno uno degli angoli acuti congruenti, essi sono sicuramente due triangoli SIMILI. Ricordiamo che due poligoni si dicono simili quando hanno gli angoli corrispondenti ordinatamente congruenti e i lati corrispondenti proporzionali.
Quindi possiamo dire che i lati dei nostri due triangoli sono proporzionali. Cioè possiamo scrivere:
AT : OA = HP : OH
Ora osserviamo che:
- AT non è altro che la tangente dell'angolo α;
- OA è il raggio della circonferenza goniometrica e, quindi, è pari a 1;
- HP è il seno dell'angolo α;
- OH è il coseno dell'angolo α.
Quindi possiamo scrivere:
AT = tan α
OA = 1
HP = sen α
OH = cos α.
E dato che
AT : OA = HP : OH
possiamo scrivere:
tan α : 1 = sen α : cos α
da cui
tan · cos α = 1 · sen α
da cui ricaviamo la tangente dell'angolo α:
tan α = sen α/cos α
In altre parole la TANGENGE dell'angolo α può essere definita anche come il RAPPORTO tra il SENO e il COSENO dell'angolo α.
Quella che abbiamo appena visto si chiama SECONDA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA.
Come abbiamo avuto modo di dire nella lezione precedente il valore della TANGENTE di α NON è DEFINITO quando
α = ±90° + k·360°
con k ∈ Z
cioè quando
α = ±π/2 + 2kπ radianti
Questa affermazione è vera anche se definiamo la tangente come rapporto tra seno e coseno dell'angolo.
Vediamolo attraverso un esempio:
Quando
α = 90°
avremo che:
sen α = 1
cos α = 0
da cui:
tan α = sen α / cos α = 1/0
che è una frazione impossibile.
Chiaramente potremmo andare avanti con gli esempi per dimostrare che questa affermazione è vera ogni volta che α = ±90° + k·360°.






