PROPRIETA' DEGLI ANGOLI ALLA CIRCONFERENZA
- La circonferenza e il cerchio
- Archi di una circonferenza
- Angoli al centro
- Angoli alla circonferenza
- Angoli alla circonferenza particolari
- Angoli al centro e angoli alla circonferenza
- Proprietà degli angoli alla circonferenza
- Proprietà degli angoli alla circonferenza
- Proprietà degli angoli alla circonferenza
Disegniamo una CIRCONFERENZA di centro O e raggio r:
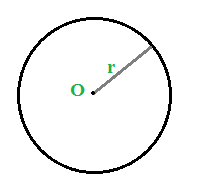
Ora disegniamo un qualsiasi ARCO
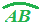 :
:
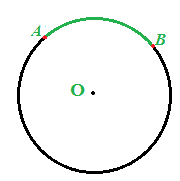
Disegniamo l'ANGOLO AL CENTRO che insiste su tale arco:
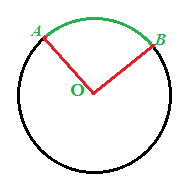
E adesso disegniamo uno degli infiniti ANGOLI alla CIRCONFERENZA che insistono su tale arco:
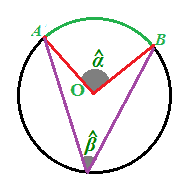
Ora, se misuriamo con un goniometro, i
due angoli 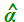 e
e
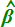 noteremo che l'angolo Alfa ha un'ampiezza
DOPPIA rispetto all'ampiezza dell'angolo Beta.
noteremo che l'angolo Alfa ha un'ampiezza
DOPPIA rispetto all'ampiezza dell'angolo Beta.
In altre parole possiamo scrivere che:
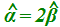
oppure che
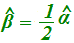
Se proviamo a disegnare ogni altro angolo alla circonferenza che insiste su tale arco giungeremo alla stessa conclusione.
E noteremo la stessa cosa anche disegnando degli altri archi, gli angoli al centro che insistono su di esso e un qualsiasi angolo alla circonferenza che insiste sullo stesso arco.
Quindi possiamo affermare che in una qualsiasi circonferenza OGNI ANGOLO alla CIRCONFERENZA è la META' dell'ANGOLO al CENTRO che insiste sullo stesso arco.
Nella lezione successiva continueremo ad esaminare altre proprietà degli angoli alla circonferenza.






