ANGOLI ALLA CIRCONFERENZA PARTICOLARI
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- La circonferenza e il cerchio
- Corde di una circonferenza
- Angoli alla circonferenza
- Posizioni di una retta rispetto ad una circonferenza
- Il punto
- La semiretta
- Rette perpendicolari
- Gli angoli
- Angolo retto - angolo acuto - angolo ottuso
Nella lezione precedente abbiamo esaminato un caso particolare di ANGOLO ALLA CIRCONFERENZA. Abbiamo visto il caso in cui l'angolo alla circonferenza è formato da due semirette uscenti per un punto P della circonferenza di cui una è SECANTE e l''altra TANGENTE alla circonferenza.
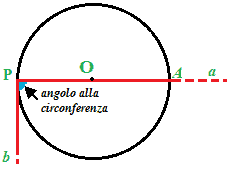
Esaminiamo meglio questo caso.
Osserviamo che uno dei LATI dell'angolo alla circonferenza è il DIAMETRO.
Inoltre l'angolo alla circonferenza
insiste sull'arco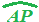 
che coincide con la SEMICIRCONFERENZA.
Infine, dato che il DIAMETRO e la TANGENTE sono PERPENDICOLARI, l'ANGOLO ALLA CIRCONFERENZA è un ANGOLO RETTO, cioè un angolo che misura 90°.
