RAPPRESENTAZIONE DI UN PUNTO SU UN PIANO CARTESIANO
- Assi cartesiani ortogonali
- Il punto
- Il piano
- Il segmento
- Rette perpendicolari
- Figure geometriche equivalenti e figure geometriche congruenti
- Misure di lunghezza
Nella lezione precedente ci eravamo posti come obiettivo quello di rappresentare un punto su un piano cartesiano.
Ora che conosciamo gli ASSI CARTESIANI ORTOGONALI vediamo come possiamo fare.
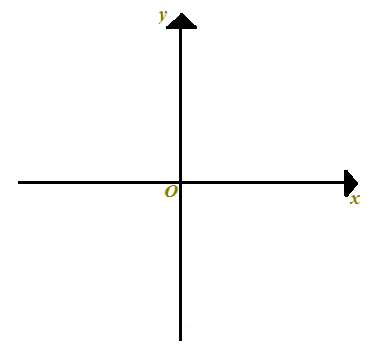
Riprendiamo i nostri assi cartesiani ed indichiamo semplicemente:
- con una x l'asse delle ascisse;
- con una y l'asse delle ordinate.
Fissiamo una unità di misura per le lunghezze, ad esempio, un segmento
OA = u
e riportiamo tale segmento sui due assi:
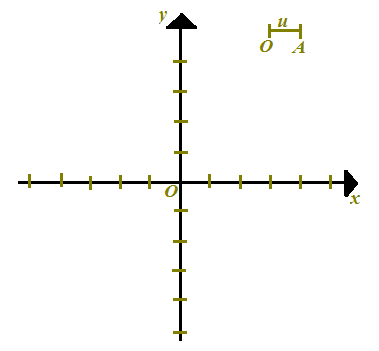
Ora, decidiamo di assegnare all'origine degli assi il valore zero.
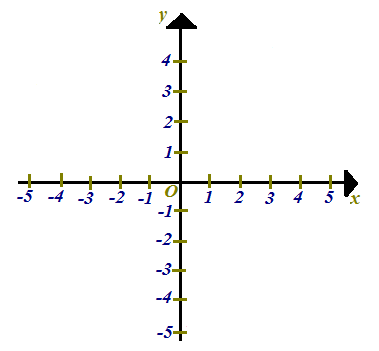
Ai punti situati sul semiasse positivo delle ascisse assegneremo i valori +1, +2, +3, +4, ecc...
Ai punti situati sul semiasse negativo delle ascisse assegneremo i valori -1, -2, -3, -4, ecc...
I valori, sull'asse delle ascisse, crescono spostandosi da sinistra verso destra.
Ai punti situati sul semiasse positivo delle ordinate assegneremo i valori +1, +2, +3, +4, ecc..
Ai punti situati sul semiasse negativo delle ordinate assegneremo i valori -1, -2, -3, -4, ecc..
I valori, sull'asse delle ordinate, crescono spostandosi dal basso verso l'alto.
Ora disegniamo un punto P nel piano:
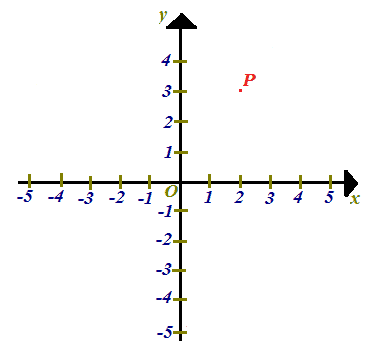
Conduciamo, dal punto P, le perpendicolari PH e PK rispettivamente all'asse delle x e all'asse delle y:
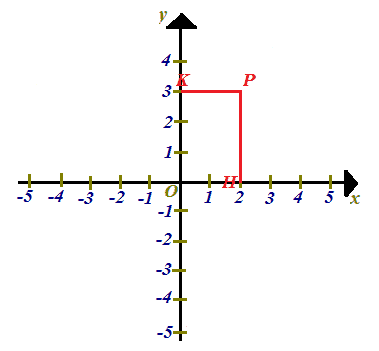
Osserviamo ora il segmento OH. Esso è congruo al segmento KP.
Allo stesso modo il segmento OK è congruo al segmento HP.
Quindi OH e OK si dicono rispettivamente ASCISSA e ORDINATA del punto P.
Entrambe prendono il nome di COORDINATE del punto P.
L'ascissa e l'ordinata di un punto si prendono con segno positivo, o con segno negativo, a seconda che i segmenti OH e OK appartengono al semiasse positivo o al semiasse negativo.
Nel nostro esempio il punto P ha coordinate:
- OH, cioè 2, che è l'ascissa;
- e OK, cioè 3, che è l'ordinata.
Per indicare le COORDINATE del punto P si scrive:
P (2; 4)
che si legge
punto P di coordinante 2 e 4
Nella lezione successiva vedremo vari esempi su come possiamo rappresentare un punto su un piano cartesiano.






