FORMULA DI DUPLICAZIONE DELLA TANGENTE
- Seconda relazione fondamentale della goniometria
- Formule goniometriche
- Formula di duplicazione del seno
- Formula di duplicazione del coseno
Nella lezione precedente abbiamo visto qual è la FORMULA DI DUPLICAZIONE DELLA TANGENTE e come si giunge ad essa.
Sempre nella precedente lezione abbiamo detto che esiste un altro modo per dimostrare come si giunge alla formula di duplicazione della tangente.
In questa lezione andremo a vedere questo secondo metodo.
Come sempre, iniziamo con lo scrivere:
tan 2α
La seconda relazione fondamentale della goniometria ci dice che la TANGENTE di un angolo non è altro che il RAPPORTO tra il SENO e il COSENO dello stesso angolo. Quindi possiamo scrivere:
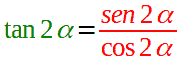
La formula di duplicazione del seno ci dice che:
sen 2α = 2 sen α · cos α
mentre la formula di duplicazione del coseno ci dice che:
cos 2α = cos2 α - sen2 α
Per cui, sostituendo nella precedente, possiamo scrivere:
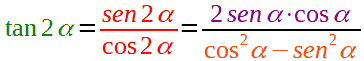
Ovviamente, trattandosi di una frazione, dobbiamo porre come condizione che il denominatore sia diverso da zero, affinché la frazione abbia significato. Quindi, la condizone da porre è:
cos2 α - sen2 α ≠ 0
Ovviamente questa condizione si verifica quando:
cos2 α ≠ sen2 α
cioè quando:
cos α ≠ sen α
Abbiamo già visto nella lezione precedente, a cui rimandiamo, che questa condizone equivale a dire che:
α ≠ ± (π/4) + kπ
con k ∈ Z
Ora torniamo alla nostra formula
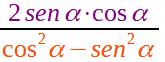
e andiamo a dividere, numeratore e denominatore, per cos2 α:
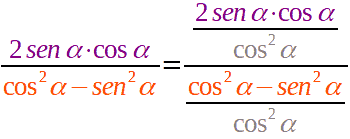
da cui otteniamo:
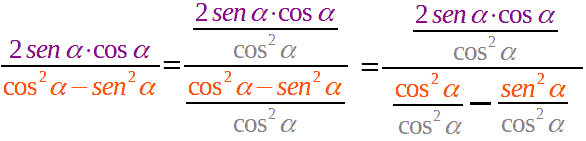
Semplificando, avremo:
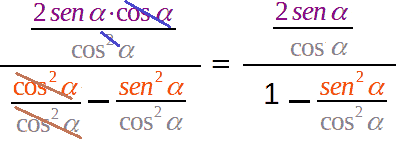
Poiché abbiamo diviso numeratore e denominatore per il cos2 α dobbiano porre come ulteriore condizione che :
cos2 α ≠ 0
che equivale a dire
cos α ≠ 0
Come abbiamo visto nella lezione precedente questa condizone equivale a dire che:
α ≠ (π/2) + kπ
con k ∈ Z
Ora, ricordando che il rapporto tra il seno e il coseno di un angolo non è altro che la tangente dell'angolo stesso, riscriviamo la formula di duplicazione della tangente nel modo seguente:

poste le seguenti condizioni di esistenza
α ≠ ± π/4 + kπ
α ≠ (π/2) + kπ
con k ∈ Z
Come possiamo notare, si tratta esattamente della stessa formula a cui eravamo giunti nella precedente lezione.






