FORMULA PARAMETRICA DEL COSENO
- Prima relazione fondamentale della goniometria
- Seconda relazione fondamentale della goniometria
- Formula di duplicazione del coseno
Dopo aver parlado della formula paramentrica del seno, ora ci occuperemo della FORMULA PARAMENTRICA DEL COSENO.
Come di consueto scrivamo il coseno dell'angolo α come
cos α = cos 2 · α/2
La FORMULA DI DUPLICAZIONE DEL COSENO ci dice che:
cos 2α = cos2 α - sen2 α
Andiamo a sostituire questa formula nella precedente:

Ora vogliamo trasformare il secondo membro in una frazione: per farlo, lo andiamo a dividere per 1.

La PRIMA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA ci dice che la SOMMA del SENO AL QUADRATO di un angolo e del COSENO AL QUADRATO dello stesso angolo è uguale a 1. Quindi
sen2 α/2 + cos2 α/2 = 1
Di conseguenza possiamo scrivere il denominatore della nostra frazione come:

A questo punto dividiamo numeratore e denominatore per cos 2 α/2.
Ovviamente, prima di eseguire la divisione dobbiamo porre come condizione che
cos2 α/2 ≠ 0
da cui ricaviamo
cos α/2 ≠ 0
e noi sappiamo che ciò accade quando l'angolo misura 90°, 270°, ecc..
In altre parole la condizione da porre è
α/2 ≠π/2 + kπ
e moltiplicando tutto per due, la nostra condizione diventa:
α ≠ π + 2kπ
Torniamo alla nostra formula che, dopo la divisione, si presenta così:

Andiamo a scriverla nel modo seguente:

Semplifichiamo:

Ora, ricordando che:
- il COSENO di 2 α/2 non è altro che il cos α;
- la SECONDA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA ci dice che la TANGENTE non è altro che il RAPPORTO tra il SENO e il COSENO dell'angolo
possiamo scrivere:
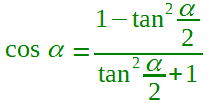
e modificando l'ordine diventa

Ovviamente dobbiamo ricordarci di porre la condizione
α/2 = π/2 + kπ
con k ∈ Z
Spesso, per una questione di praticità, si pone:
t = tan α/2
per cui la formula diventa:







