PRIMA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Seno e coseno
• Funzioni goniometriche fondamentali

Disegniamo la circonferenza goniometrica e l'angolo orientato α.

Ora individuiamo il COSENO dell'angolo α:

e il SENO dell'angolo α:

Il triangolo PHO è un TRIANGOLO RETTANGOLO in H (in altre parole H è l'angolo retto).

Trattandosi di un triangolo rettangolo possiamo applicare il TEOREMA DI PITAGORA e scrivere:

L'IPOTENUSA del nostro triangolo, non è altro che il RAGGIO della circonferenza goniometrica. Noi sappiamo che il RAGGIO della circonferenza goniometrica è uguale ad 1, quindi possiamo scrivere:

da cui segue che:

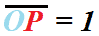
La misura del cateto PH non è altro che il VALORE ASSOLUTO dell'ORDINATA del punto P, cioè

|y_P|

E poiché il quadrato di un numero è sempre positivo, possiamo dire che

|y_P|² = y_P²

.

Ma noi sappiamo anche che l'ordinata del punto P non è altro che il SENO dell'angolo α, quindi:

y_P² = sen α

.

In maniera analoga possiamo dire che la misura del cateto OH non è altro che il VALORE ASSOLUTO dell'ASCISSA del punto P, cioè

|x_P|

.

E poiché il quadrato di un numero è sempre positivo, possiamo dire che

|x_P|² = x_P²

.

Ma noi sappiamo anche che l'ascissa del punto P non è altro che il COSENO dell'angolo α, quindi:

x_P² = cos α

.

Di conseguenza possiamo scrivere:

sen² α + cos² α = 1.

Quella che abbiamo appena scritto è la PRIMA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA.

Quindi la prima relazione fondamentale della goniometria è una relazione che lega il seno e il coseno di uno stesso angolo. In base ad essa sappiamo che la SOMMA dei QUADRATI del SENO e del COSENO di uno stesso angolo sono sempre UGUALI all'UNITA'.

Chiaramente, da essa, desumiamo che

sen² α = 1 - cos² α

per trovare il seno dell'angolo α estraiamo la radice quadrata dal primo e dal secondo membro ricordandoci di prendere sia il valore positivo che quello negativo del risultato trovato

Allo stesso modo avremo che:

cos² α = 1 - sen² α

per trovare il coseno dell'angolo α estraiamo la radice quadrata dal primo e dal secondo membro ricordandoci. anche in questo caso. di prendere sia il valore positivo che quello negativo del risultato trovato

Nella prossima lezione faremo delle precisazioni su come vanno scritte le potenze della funzione seno e della funzione coseno.

Lezione precedente - Lezione successiva

Indice degli argomenti sulle funzioni goniometriche

Pubblicità/Advertising