BARICENTRO
- Triangoli
- Elementi del triangolo
- Triangolo rettangolo
- Elementi e punti notevoli di un triangolo
- Mediane
Nella lezione precedente abbiamo visto che le tre mediane di un triangolo passano tutte per uno stesso punto detto BARICENTRO e indicato, nel disegno sottostante, con la lettera O.
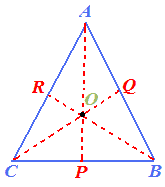
Quindi il BARICENTRO di un triangolo può essere definito come il PUNTO DI INTERSEZIONE delle tre MEDIANE del triangolo.
Possiamo provare a disegnare vari tipi di triangoli: rettangoli, ottusangolo, ecc... Noteremo che il BARICENTRO è sempre INTERNO al triangolo.
Facciamo ora un'osservazione.
Come possiamo notare dalla figura precedente, il BARICENTRO DIVIDE ogni MEDIANA in DUE PARTI:
- la mediana QC è divisa nei segmenti QO e OC;
- la mediana RB è divisa nei segmenti RO e OB;
- la mediana AP è divisa nei segmenti AO e OP.
Proviamo ora a misurare con un righello questi segmenti. Noteremo che per ogni mediana, uno dei due segmenti nei quali risulta diviso dal baricentro è doppio dell'altro segmento.
In altre parole avremo che:
OC = 2QO
OB = 2RO
OP
= 2AO.
Ciò si verifica per qualsiasi triangolo disegnato.
Possiamo
allora affermare che, in ogni triangolo, il BARICENTRO
divide ogni MEDIANA
in DUE PARTI che sono UNA
DOPPIA DELL'ALTRA.
La parola BARICENTRO significa "centro del peso", in altre parole esso è l'unico punto di equilibrio di un triangolo.
Possiamo dimostrare quanto affermato disegnando un triangolo su un cartoncino rigido. Ritagliamo ora il triangolo e disegniamo il suo baricentro. Facciamo passare per questo punto un cordoncino: vedremo che il triangolo starà in equilibrio.
Se proviamo ad appendere il cordoncino in qualsiasi altro punto del triangolo, invece, esso non sarà in equilibrio.






