BISETTRICI
- Triangoli
- Elementi del triangolo
- Triangolo rettangolo
- Elementi e punti notevoli di un triangolo
- Gli angoli
- Bisettrice di un angolo
Dallo studio degli ANGOLI abbiamo appreso che si chiama BISETTRICE DI UN ANGOLO la SEMIRETTA che ha per ORIGINE il VERTICE dell'angolo e che divide l'angolo in DUE PARTI UGUALI e abbiamo anche visto come è possibile disegnarla.
Ora disegniamo il triangolo ABC:
Quindi disegniamo un segmento che partendo dell'angolo A raggiunga il lato opposto BC, dividendo l'angolo A in due parti aventi la stessa ampiezza:
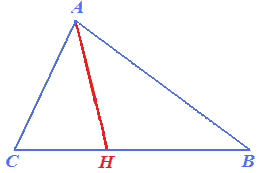
Il segmento AH che abbiamo disegnato prende il nome di BISETTRICE di VERTICE A del triangolo.
Quindi possiamo dire che la BISETTRICE di un triangolo RELATIVA AD UN VERTICE è il SEGMENTO che UNISCE il VERTICE al LATO OPPOSTO DIVIDENDO a META' l'angolo.
Ora disegniamo anche la bisettrice del triangolo relativa al vertice B e la bisettrice del triangolo relativa al vertice C:
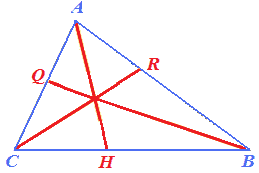
Come possiamo osservare le TRE BISETTRICI si INCONTRANO in un punto detto INCENTRO che nel nostro disegno abbiamo evidenziato con la lettera O:
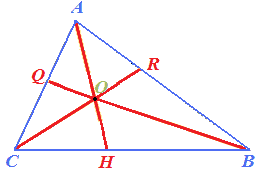
Qualsiasi triangolo noi disegniamo l'INCENTRO è sempre INTERNO al triangolo.






