CLASSIFICAZIONE DEI QUADRILATERI
- Quadrilateri
- I poligoni
- Caratteristiche dei poligoni
- Figure geometriche equivalenti e figure geometriche congruenti
- Confronto di segmenti
- Rette parallele
Nella lezione precedente abbiamo appreso che un QUADRILATERO è un POLIGONO che ha QUATTRO LATI e QUATTRO ANGOLI.
I QUADRILATERI possono essere classificati a seconda delle caratteristiche dei loro LATI e dei loro ANGOLI.
| TIPO | IMMAGINE |
|---|---|
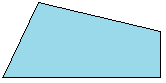
| Il quadrilatero con 4 LATI GENERICI, cioè senza particolari proprietà, si dice QUADRILATERO SCALENO. |
|
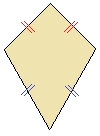
| Il
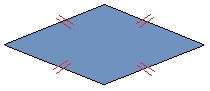
quadrilatero con 2 COPPIE di LATI
CONSECUTIVI CONGRUENTI si dice DELTOIDE.
Ricordiamo che DUE LATI di un poligono si dicono CONSECUTIVI se hanno un VERTICE IN COMUNE. Mentre due segmenti si dicono CONGRUENTI quando hanno la STESSA LUNGHEZZA. |
Nella figura sopra abbiamo segnato in rosso due dei lati consecutivi congruenti e in blu, gli altri due. |
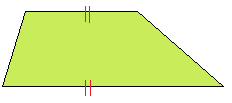
| Il quadrilatero con
1 COPPIA di LATI OPPOSTI PARALLELI si dice
TRAPEZIO.
Ricordiamo che due rette si dicono PARALLELE quando appartengono allo stesso piano e NON HANNO NESSUN PUNTO IN COMUNE. |
Nella figura sopra abbiamo segnato in rosso i due lati opposti paralleli. |
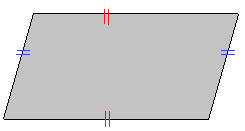
| Il TRAPEZIO che ha ENTRAMBE le COPPIE DI LATI OPPOSTI PARALLELI e CONGRUENTI prende il nome di PARALLELOGRAMMA. |
Nella figura sopra abbiamo segnato in rosso due lati opposti paralleli e in blu, gli altri due. |
| Il PARALLELOGRAMMA che ha QUATTRO ANGOLI CONGRUENTI, cioè di uguale ampiezza, prende il nome di RETTANGOLO. |
|
| Il PARALLELOGRAMMA che ha QUATTRO LATI CONGRUENTI, cioè aventi tutti la stessa lunghezza ampiezza, prende il nome di ROMBO. |
|
| Il PARALLELOGRAMMA che ha QUATTRO ANGOLI CONGRUENTI e QUATTRO LATI CONGRUENTI, prende il nome di QUADRATO. |
|