DIAGONALI DEL PARALLELOGRAMMA
- Parallelogramma
- Parallelogramma: definizioni
- Proprietà del parallelogramma
- Diagonali del parallelogramma
- Lati del parallelogramma
- Angoli del parallelogramma
- Angoli adiacenti del parallelogramma
- Diagonale di un poligono
- Triangoli
- Figure geometriche equivalenti e figure geometriche congruenti
Disegniamo su un cartoncino il PARALLELOGRAMMA ABCD:
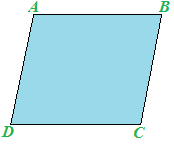
Ora disegniamo una delle DIAGONALI del parallelogramma. Ad esempio la diagonale AC:
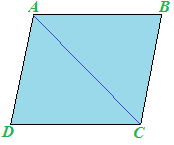
Ritagliamo il parallelogramma e, successivamente, ritagliamo lungo la diagonale AC. Otterremo due triangoli, ABC e ACD che nell'immagine abbiamo evidenziato con colori diversi:
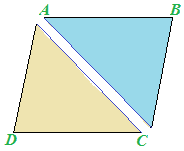
Sovrapponiamo uno di essi sull'altro. Vedremo che i due triangoli sono congruenti:
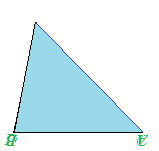
Quindi possiamo scrivere:
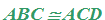
che si legge
il triangolo ABC è congruente al triangolo ACD.
Ora proviamo a disegnare l'altra diagonale BD. Ritagliamo i due triangoli ottenuti e sovrapponiamoli l'uno all'altro. Noteremo che, anche in questo caso, i due triangoli ottenuti sono congruenti.
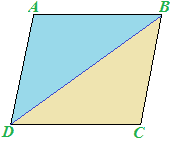
Quindi possiamo scrivere:
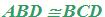
che si legge
il triangolo ABD è congruente al triangolo BCD.
Di conseguenza possiamo affermare che ogni PARALLELOGRAMMA è DIVISO da ciascuna DIAGONALE in DUE TRIANGOLI CONGRUENTI.






