DIAGONALI DEL PARALLELOGRAMMA
- Parallelogramma
- Parallelogramma: definizioni
- Proprietà del parallelogramma
- Diagonali del parallelogramma
- Lati del parallelogramma
- Angoli del parallelogramma
- Angoli adiacenti del parallelogramma
- Diagonale di un poligono
- Triangoli
- Figure geometriche equivalenti e figure geometriche congruenti
Nella lezione precedente abbiamo visto che che ogni PARALLELOGRAMMA è DIVISO da ciascuna DIAGONALE in DUE TRIANGOLI CONGRUENTI.
Ora disegniamo un PARALLELOGRAMMA ed entrambe le DIAGONALI.
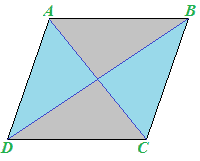
Le due diagonali si INTERSECANO nel punto O:
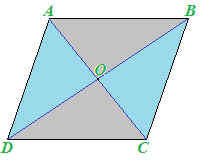
Notiamo che si formano così 4 triangoli.
Ora ritagliamo il triangolo AOB e sovrapponiamolo al triangolo DOC:
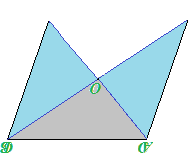
I due triangoli sono perfettamente sovrapponibili, quindi sono CONGRUENTI.
Se i due triangoli sono congruenti, anche i loro LATI sono CONGRUENTI.
Quindi:
- il lato AO del primo triangolo è congruente con il lato OC del secondo triangolo;
- il lato BO del primo triangolo è congruente con il lato OD del secondo triangolo.
Ma se il segmento AO e il segmento OC hanno la stessa lunghezza, significa che il punto O divide esattamente a metà la diagonale AC.
Allo stesso modo, se il segmento BO e il segmento OD hanno la stessa lunghezza, significa che il punto O divide esattamente a metà la diagonale BD.
Questo significa che in ogni parallelogramma le DIAGONALI si TAGLIANO a META'.






