TRASLAZIONE DEGLI ASSI CARTESIANI
Disegniamo il SISTEMA DI ASSI CARTESIANI xOy:
Disegniamo ora il punto P, tale che
P (x; y).
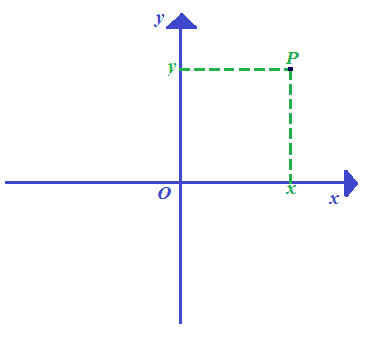
Ora immaginiamo che il SISTEMA DI ASSI CARTESIANI, venga TRASLATO, cioè:
- si porta l'origine degli assi in O1
tale che
O1 (p, q);
-
lasciando gli ASSI PARALLELI ai precedenti.
Iniziamo col disegnare il punto O1:
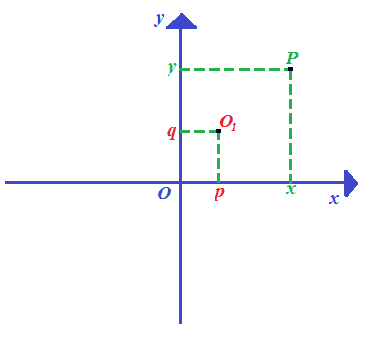
Ora disegniamo gli assi che hanno origine nel punto O1 e li indichiamo con X e Y:
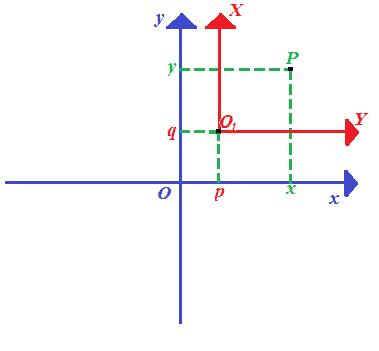
Ora vogliamo vedere come variano le coordinate del punto P, cioè quali sono le COORDINATE del punto P nel momento in cui gli ASSI sono TRASLATI.
Per rendere più comprensibile l'esposizione chiameremo i punti individuati con le lettere A, B, C, D come illustrato nell'immagine che segue:
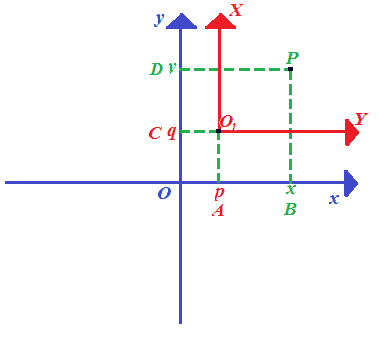
Andiamo a vedere quali sono le coordinate di P sul sistema di assi XO1Y.
Osserviamo che:
- OB (cioè l'ascissa del punto P sul sistema di assi xOy) è pari a OA (cioè l'ascissa del punto O1 sul sistema di assi xOy) + AB (cioè l'ascissa del punto P sul sistema di assi XO1Y);
- OD (cioè l'ordinata del punto P sul sistema di assi xOy) è pari a OC (cioè l'ordinata del punto O1 sul sistema di assi xOy) + CD (cioè l'ordianta del punto P sul sistema di assi XO1Y).
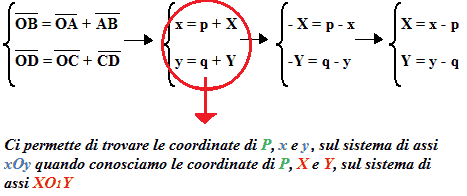
Per questa ragione possiamo scrivere:
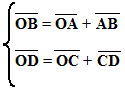
Ora chiamiamo con X maiuscolo e Y maiuscolo le coordinate di P riferite al sistema di assi XO1Y e otteniamo:
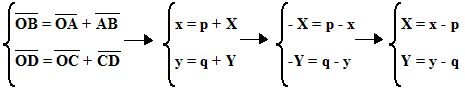
Notiamo che:
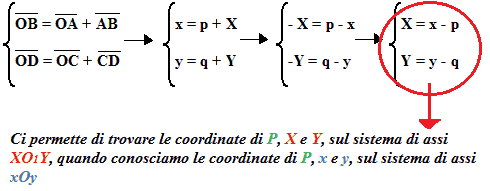
Esempio 1:
sia P (-2; 3) un punto riferito ad un sistema di assi cartesiani xOy. Quali sono le coordinate di tale punto quando il sistema viene traslato con origine in O1 (3; -1)?
Applicheremo le formule:
X = x- p = -2 - (3) = -2 -3 = -5
Y = y - q = 3 - (-1) = 3 + 1 = 4.
Le coordinate cercate sono -5 e 4.
Esempio 2:
sia P un punto riferito ad un sistema di assi cartesiani xOy. Traslando gli assi in modo che questi abbiamo origine in O1 (-2; 5) il punto P ha coordinate (5; -4). Quali sono le coordinate del punto P sul sistema di assi xOy?
Applicheremo le formule:
x = p + X = -2 + 5 = 3
y = q+ Y = 5 + (-4) = 5 - 4 = 1.
Le coordinate cercate sono 3 e 1.






