PUNTI SIMMETRICI RISPETTO ALL'ORIGINE DEGLI ASSI
- Punti simmetrici rispetto ad un punto
- Il punto
- Assi cartesiani ortogonali
- Il segmento
- Confronto di segmenti
- Coordinate del punto medio di un segmento
- I numeri relativi
Nella lezione precedente abbiamo appreso quando due PUNTI sono SIMMETRICI rispetto ad un punto.
Ora, supponiamo di avere il punto A1 tale che
A1 (x1; y1).
Disegniamo, questo punto, sugli assi cartesiani:
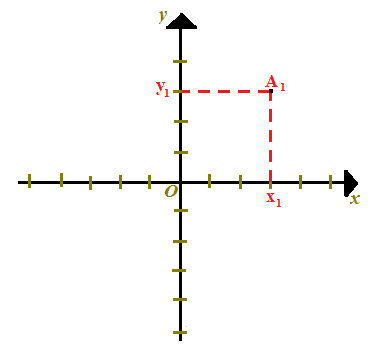
Ora vogliamo trovare il punto A2 che sia SIMMETRICO al punto A1 rispetto all'ORIGINE degli ASSI CARTESIANI che abbiamo chiamato O.
Affinché A1 e A2 siano simmetrici rispetto ad O è necessario che:
- i punti A1, O e A2 siano ALLINEATI;
- i segmenti A1O e OA2 siano CONGRUENTI.
Quindi, graficamente, avremo:
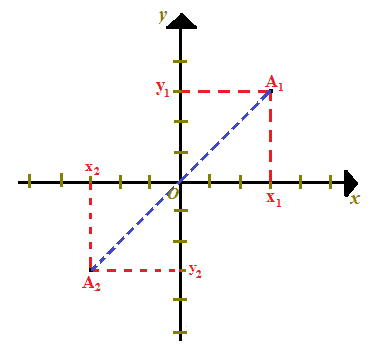
Cerchiamo di capire quali sono le coordinate del punto A2.
Poiché i punti A1 e A2 sono simmetrici rispetto all'origine, i segmenti A1O e OA2 sono congruenti. Di conseguenza l'ORIGINE DEGLI ASSI, O, non è altro che il PUNTO MEDIO dei punti A1 e A2.
Noi sappiamo che il PUNTO MEDIO ha le seguenti coordinate:

E sappiamo anche che l'origine degli assi ha coordinate
O (0; 0).
Quindi possiamo dire che:
0 = (x1 + x2)/ 2
e
0 = (y1 + y2)/ 2.
Moltiplichiamo il primo e il secondo membro di entrambe le equazioni per 2, e avremo:
0 · 2 = x1 + x2
e
0 · 2 = y1 + y2.
Da cui:
0 = x1 + x2
e
0 = y1 + y2.
Portando a primo membro x2 e y2,e cambiando di segno si avrà:
-x2 = x1
e
-y2 = y1.
Infine, cambiando di segno ad entrambi i membri delle due equazioni, scriveremo:
x2 = - x1
e
y2= - y1.
Quindi possiamo dire che il punto A2 ha:
- come ascissa l'OPPOSTO dell'ASCISSA di A1;
- come ordinata l'OPPOSTO dell'ORDINATA di A1.
Di conseguenza possiamo dire che, dato un punto
A1 (x1; y1)
il suo SIMMETRICO RISPETTO ALL'ORIGINE DEGLI ASSI A2, avrà come coordinate:
A2 (-x1; -y1).
Esempio:
dato il punto
A1 (3; -5)
determinare il punto A2, ad esso simmetrico rispetto all'origine degli assi.
Il punto A2, simmetrico di A1 rispetto all'origine degli assi, avrà:
- come ascissa, l'opposto dell'ascissa di A1;
- come ordinata, l'opposto dell'ordinata di A1.
Quindi
A2 (-3; +5).






