DISEQUAZIONI GONIOMETRICHE RICONDUCIBILI A QUELLE ELEMENTARI
Vediamo, in questa lezione, un esempio di DISEQUAZIONI GONIOMETRICHE RICONDUCIBILI a quelle ELEMENTARI.
Si tratta di disequazioni del tipo:
sen f(x) > m
dove
f(x) è una funzione contenente l'incognita x
mentre
m è una costante.
Chiaramene al posto del seno possiamo avere una qualsiasi altra funzione goniometrica (coseno, tangente, cotangente...) e al posto del segno uguale possiamo avere il segno minore, maggiore-uguale, minore-uguale.
Risolviamo la disequazione:
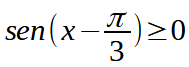
Per prima cosa osserviamo che non dobbiamo porre nessuna condizione di esistenza dato che il seno è sempre definito.
Poniamo:
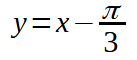
Otterremo:
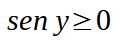
Ora noi sappiamo che il seno di un angolo assume valori positivi quando l'angolo è compreso tra 0 e π.
Quindi la soluzione della disequazione è:
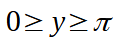
Ora, sostituendo ad y la funzione di partenza, ovvero x - π/3, avremo:
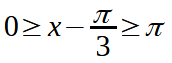
Per trovare il valore di x aggiungiamo, membro a membro, +π/3, in modo da avere:
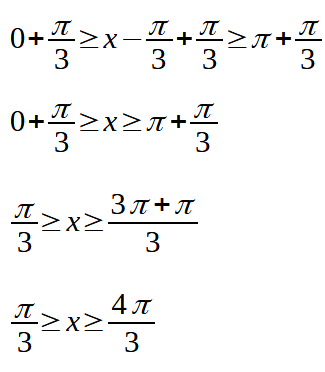
Ora tenuto conto che la periodicità della funzione seno è 2π, la soluzione della nostra disequazione diventa: