DISEQUAZIONI GONIOMETRICHE NON ELEMENTARI
Per DISEQUAZIONI GONIOMETRICHE NON ELEMENTARI si intendono tutte le disequazioni goniometriche che si presentano in una FORMA DIVERSA da quelle ELEMENTARI.
In alcuni casi non dobbiamo farci ingannare dall'apparenza, in quanto alcune disequazioni che potrebbero, a prima vista, sembrare non elementari, in realtà sono tali. Ad esempio se dobbiamo risolvere la disequazione:
sen x - 1 > 0
basta spostare l'1 a secondo membro cambiandogli di segno, fare la somma algebrica con lo zero e avremo una disequazione elementare:
sen x > 1
Oppure se abbiamo la disequazione:
2 cos x < 1
basta dividere entrambi i membri per 2 ed avremo la disequazione elementare:
cos x < 1/2
Ancora, se ci troviamo di fronte alla disequazione:
2 tan x + 4 > tan x + 4
basta portare a primo membro la tangente di x, cambiandogli di segno, e portare a secondo membro 4, cambiandogli di segno, ed eseguire le somme algebriche, e avremo ottenuto una disequazione goniometrica elementare:
2 tan x - tan x > 4 - 4
tan x > 0
Quindi, queste sono disequazioni che, con alcuni semplici passaggi, possono essere scritte come disequazioni goniometriche elementari.
Ricordiamoci sempre, prima di risolverle, di porre le CONDIZIONI DI ESISTENZA.
Vediamo, ora, alcuni tipi di disequazioni goniometriche NON ELEMENTARI ricordandoci sempre che, come prima cosa, occorre porre le CONDIZIONI DI ESISTENZA della disequazione e, una volta ottenuti i risultati, occorre verificare che essi siano compatibili con tali condizioni.
1 - DISEQUAZIONI GONIOMETRICHE RICONDUCIBILI A QUELLE ELEMENTARI
Rientrano in questa casistica disequazioni del tipo:
sen f(x) > m
Chiaramente, in questo come negli esempi che faremo in seguito, al posto del seno potremmo avere una qualsiasi altra funzione goniometrica e, al posto del segno maggiore, potremmo avere il segno minore oppure maggiore-uguale o ancora minore-uguale.
Queste disequazioni si risolvono per SOSTITUZIONE, ovvero si pone:
y = f(x)
e si risolve la disequazione
sen y > m
Una volta trovato il valore di y si trova il valore di x e si tiene conto della periodicità dalla funzione per avere i risultati della disequazione.
(Per un esempio di risoluzione di una disequazione goniometrica riconducibile a quelle elementari si veda la lezione 10).
2 - DISEQUAZIONI GONIOMETRICHE RICONDUCIBILI AD UN POLINOMIO
Questo tipo di disequazioni è caratterizzato dalla presenza di una sola funzione goniometrica ripetuta più volte con potenze diverse. Esempio:
a sen2 x + b sen x + c > 0
Anche queste disequazioni si risolvono mediante una SOSTITUZIONE. Occorrerà porre:
y = sen x
e risolvere la disequazione:
ay2 + by + c > 0
Una volta trovato il valore di y, tenendo conto che y = sen x, si trova il valore di x. Infine si tiene conto della periodicità dalla funzione per avere i risultati della disequazione.
(Per un esempio di risoluzione di una disequazione goniometrica riconducibile ad un polinomio si veda la lezione 11).
3 - DISEQUAZIONI GONIOMETRICHE FRATTE O SOTTO FORMA DI PRODOTTO
Un altro gruppo di disequazioni goniometriche non elementari è costituito da DISEQUAZIONI FRATTE, che presentano delle funzioni goniometriche sia a numeratore che a denominatore.
Questo tipo di disequazioni si risolve come tutte le disequazioni fratte, ovvero STUDIANDO il SEGNO del numeratore e del denominatore e andando a cercare i valori di x che soddisfano la disequazione. Ovviamente dobbiamo ricordaci, come in tutte le disequazioni fratte, di porre una ulteriore CONDIZIONE DI ESISTENZA, ovvero di escludere dalle soluzioni i valori di x che ANNULLANO il DENOMINATORE.
In questo stesso gruppo possiamo far rientrare le disequazioni goniometriche scritte sotto forma di PRODOTTO di due o più fattori nei quali sono presenti delle funzioni goniometriche.
Anche queste disequazioni si risolvono, STUDIANDO il SEGNO dei diversi fattori e andando a cercare i valori di x che soddisfano la disequazione.
(Per un esempio di risoluzione di una disequazione goniometrica fratta o sotto forma di prodotto si veda la lezione 12).
4 - DISEQUAZIONI LINEARI IN SENO E COSENO
In questa categoria rientrano delle disequazioni di primo grado nelle quali compaiono sia il seno che il coseno dello stesso angolo. Esse si presentano in questo modo:
a sen x + b cos x > c
Questo tipo di disequazioni si risolve applicando le FORMULE PARAMETRICHE, cioè quelle formule che ci permettono di esprimere il seno e il coseno di un angolo α in funzione della tangente dell'angolo α/2.
Poiché si sostituisce la tangente alla disequazione di partenza occorre tenere presente che ci potrebbero essere dei valori che non possono essere soluzioni della nuova disequazione, in quanto si tratta di valori nei quali la tangente non è definita, che però potrebbero essere soluzioni valide della disequazione di partenza. Pertanto è necessario verificare che le soluzioni non ammissibili della nuova disequazione, siano o non siano, delle soluzioni accettabili della disequazione di partenza: ciò viene fatto per sostituzione, in altre parole andando a sostituire, i valori per i quali la tangente non è definita, nella disequazione di partenza in modo da verificare se essi sono soluzioni accettabili o meno. In caso affermativo di tali valori si dovrà tenere conto nelle soluzioni dell'esercizio.
(Per un esempio di risoluzione di una disequazione lineare in seno e coseno si veda la lezione 13).
5 - DISEQUAZIONI OMOLOGHE DI SECONDO GRADO IN SENO E COSENO
Queste disequazioni possono avere due forme diverse:
a sen2 x + b sen x · cos x + c cos2 x > 0
oppure
a sen2 x + b sen x · cos x + c cos2 x > d
La differenza sta nel fatto che, nella prima disequazione, a secondo membro abbiamo lo 0, mentre nella seconda disequazione a secondo membro abbiamo un VALORE DIVERSO DA ZERO.
La prima disequazione si risolve dividendo primo e secondo membro per cos2 x.
Prima di procedere con la divisione occorre porre come condizione
cos2 x ≠ 0
I valori di x che annullano il denominatore, e che quindi, sicuramente non possono essere soluzioni della nuova disequazione da noi scritta potrebbero essere soluzioni della disequazione di partenza. Per saperlo occorre verificarlo mediante una SOSTITUZIONE di tali valori nella disequazione di partenza in modo da capire se essi vanno esclusi anche dalle solzioni della disequazione data oppure vanno inclusi in tali soluzioni.
Effettuando la nostra divisione la disequazione diventa:
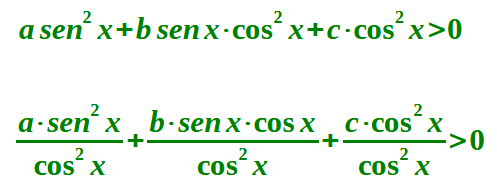
Semplificando si avrà:
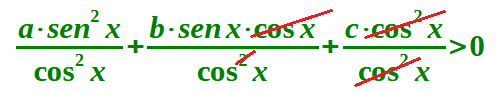
Ricordando che:
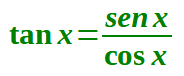
la nostra disequazione diventa:

A questo punto abbiamo ricondotto la disequazione ad una disequazione goniometrica di tipo polimoniale che abbiamo visto in precendenza.
Nel caso in cui la disequazione si presenta nella forma
a sen2 x + b sen x · cos x + c cos2 x > d
Per prima cosa andiamo a MOLTIPLICARE il secondo membro per sen2 x + cos2 x.
Noi sappiamo, dalla PRIMA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA che tale prodotto è uguale ad 1: quindi, eseguendo il prodotto non modifichiamo il valore della disequazione, ma trasformiamo la disequazione in modo da ricordurla alla forma precedente. In pratica procederemo nel modo seguente:
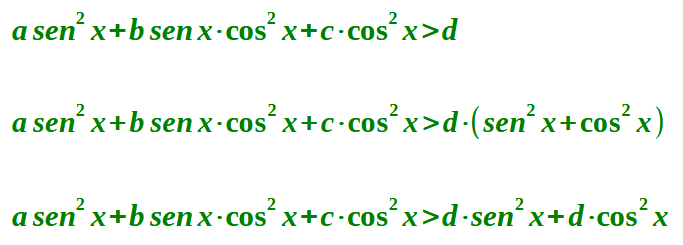
Portiamo a primo membro d · sen2 x e d · cos2 x , cambiando di segno e andiamo a sommare i termini simili:
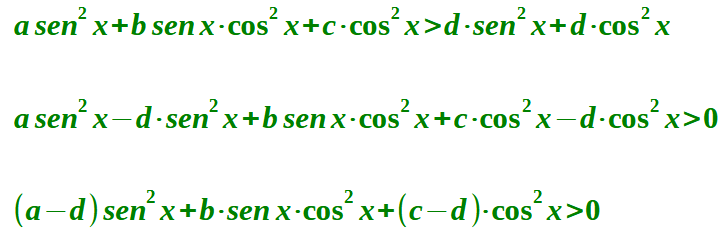
Quindi proseguiamo esattamente come abbiamo visto in precedenza.
(Per un esempio di risoluzione di una disequazione omologa di secondo grado in seno e coseno si veda la lezione 14).
6 - DISEQUAZIONI RISOLVIBILI CON LE FORMULE GONIOMETRICHE
Quando la disequazione goniometrica non è riconducibile ad uno dei casi visti in precedenza si può tentare di risolverla usando le FORMULE GONIOMETRICHE.
(Per un esempio di risoluzione di una disequazione goniometrica risolvibile con le formule goniometriche si veda la lezione 15).






