DISEQUAZIONI GONIOMETRICHE RICONDUCIBILI AD UN POLINOMIO
In questa lezione ci occuperemo di DISEQUAZIONI GONIOMETRICHE RICONDUCIBILI ad un POLINOMIO ed andremo a vedere un esempio concreto di risoluzione.
Questo tipo di disequazioni è caratterizzato dalla presenza di UNA SOLA FUNZIONE GONIOMETRICA (quindi o solo seno o solo coseno e così via) presente nella disequazione più volte e con POTENZE DIVERSE.
In pratica, questo tipo di disequazioni si presenta nella forma
a sen2 x + b sen x + c > 0
Come sempre al posto del seno possiamo avere una qualsiasi altra funzione goniometrica (coseno, tangente, cotangente...) e al posto del segno uguale possiamo avere il segno minore, maggiore-uguale, minore-uguale.
Risolviamo la disequazione:
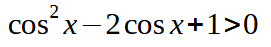
Per prima cosa vediamo se ci sono delle condizioni di esistenza da porre. Il coseno è sempre definito quindi non ci sono condizioni di esistenza da imporre prima della risoluzione della disequazione.
Per risolvere la disequazione poniamo:
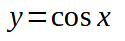
ed otteniamo:
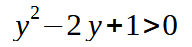
Risolviamo come una normale disequazione di secondo grado:
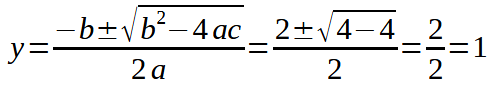
Poiché il discriminante è uguale a zero il polinomio si annulla quando y = 0 in tutti gli altri casi esso sarà maggiore di zero. Quindi, poiché noi stiamo cercando i valori di y che rendono il trinomio maggiore di zero, possiamo dire che la disequazione è verificata per qualsiasi valore di y diverso da 0.
Quindi:
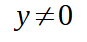
e ricordando che abbiamo posto:
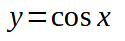
e sostituendo, abbiamo che la soluzione è data da:
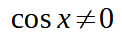
Ma noi sappiamo che il coseno di un angolo è uguale a zero quando l'angolo è pari a 0 e, successivamente, ogni 2kπ. Quindi possiamo scrivere:
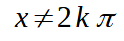
(Soluzione che comprende sia lo zero che π/2: infatti basta porre k = 0 per avere come risultato zero e k = 1 per avere come risultato 2π.)






