DISEQUAZIONI IRRAZIONALI CON LO ZERO A SECONDO MEMBRO
Iniziamo a vedere come si risolvono le DISEQUAZIONI IRRAZIONALI, partendo da quelle nelle quali compaiono:
- in un membro un POLINOMIO A(x) sotto il segno di radice;
- e nell'altro membro lo ZERO.
Si potranno avere due casi diversi:

Partiamo dal primo caso.
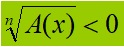
Per risolvere questo tipo di disequazioni dobbiamo distinguere due ipotesi:
- n è DISPARI;
- n è PARI.
Vediamo cosa succede quando
n è DISPARI.
Noi sappiamo che possiamo sempre estrarre la radice di indice dispari sia quando il RADICANDO è POSITIVO che quando è NEGATIVO o UGUALE A ZERO. Sappiamo anche che, nel caso in cui n è DISPARI, estraendo la radice ennesima di A(x) il valore che otterremo conserverà lo stesso segno del radicando. Quindi, sarà sufficiente che A(x) sia minore di zero che anche la sua radice sarà minore di zero.
In altre parole dovremo risolvere la disequazione:
A(x) < 0.
Vediamo ora cosa succede quando
n è PARI.
In questo caso solamente se il RADICANDO è POSITIVO o UGUALE A ZERO possiamo estrarre la sua radice. Ma sappiamo anche che, quando andiamo ad estrarre la radice, avremo sempre un valore POSITIVO o, tutt'al più, UGUALE a ZERO. Quindi non esiste un valore di x tale che A(x) risulti minore di zero. Di conseguenza la nostra disequazione NON AMMETTE SOLUZIONI.
Esempio:
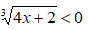
Poiché n è dispari (n = 3) e sufficiente risolvere A(x) < 0. Quindi:
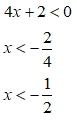
Altro esempio:
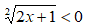
Poichè n è pari (n = 2) non ci sarà mai un valore la cui radice quadrata è negativa. Quindi la disequazione non ammette soluzioni.
Passiamo al secondo caso.
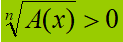
In questo caso cerchiamo il valore di x tale che la radice di A(x) sia maggiore di zero.
Se n è dispari si tratterà di cercare i valori di x che rendono A(x) positivo perché soltanto se A(x) è positivo lo è anche la sua radice di indice dispari.
Se n è pari si tratterà di cercare i valori di x che rendono A(x) positivo perché soltanto se A(x) è positivo possiamo estrarre la sua radice di indice pari ed essa sarà, a sua volta, positiva.
Quindi, in entrambi i casi, si tratterà di risolvere la disequazione:
A(x) > 0.
Esempio:
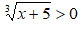
In questo caso il segno della disequazione è maggiore (>), quindi non è necessario vedere se l'indice è dispari o pari poiché, in entrambi i casi è sufficiente porre A(x) > 0. Ovvero:
x + 5 > 0
x > - 5.
E se invece del segno < o > avessimo i segni ≤ o ≥?
L'unico caso che cambia è quando il segno della disequazione è ≤ e l'indice è PARI:
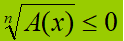
Se n è pari abbiamo detto che non esistono valori di x tali che A(x) risulti minore di zero, ma esistono valori di x tali che A(x) risulti uguale a zero. E sappiamo che la radice di zero è uguale a zero. Di conseguenza la nostra disequazione si risolve ponendo
A(x) = 0.
In tutti gli altri casi sarà sufficiente porre al posto dei simboli < o > i simboli ≤ o ≥.
Esempio:
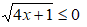
n è pari (n = 2) quindi non ci saranno valori di x tali che la radice di A(x) possa essere negativa, ma esistono valori di x tali che A(x) risulti uguale a zero e, di conseguenza, la sua radice è uguale a zero. Quindi dovremo andare a cercare le soluzioni di
4x + 1 = 0
che sarà uguale a
4x = -1
x = -1/4.
Altro esempio:
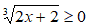
Poiché il segno della disequazione è ≥ non è importante andare a vedere se l'indice è pari o dispari e sarà sufficiente porre:
2x + 2 ≥ 0
2x ≥ -2
x ≥ -1.






