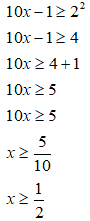DISEQUAZIONI IRRAZIONALI CON UNA COSTANTE A SECONDO MEMBRO E SEGNO DI MAGGIORE (>)
Continuiamo a vedere come si risolvono le DISEQUAZIONI IRRAZIONALI, nelle quali compaiono ad un membro un POLINOMIO, sotto il segno di radice, e all'altro una COSTANTE.
In questa lezione esamineremo il seguente caso:
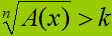
dove, lo ricordiamo,
A(x) è un polinomio
k è
una costante.
Anche in questo caso potremo avere due ipotesi diverse, a seconda del valore assunto dall'INDICE DELLA RADICE:
- n è DISPARI;
- n è PARI.
Partiamo dal caso in cui
n è DISPARI.
Se n è dispari, è sempre possibile estrarre la radice sia nell'ipotesi in cui il RADICANDO sia POSITIVO che in quella in cui esso è NEGATIVO, come pure quando il radicando è UGUALE A ZERO. Inoltre il valore ottenuto estraendo la radice avrà lo stesso segno del radicando.
Quindi, in questo caso, la disequazione viene risolta semplicemente ELEVANDO entrambi i suoi membri ad n, ovvero avremo:
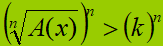
che equivale a scrivere:
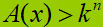
Esempio:
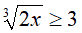
Notiamo che n è dispari (n = 3), quindi andiamo a risolvere la disequazione elevando entrambi i suoi membri alla terza:
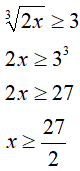
Vediamo cosa accade, invece, se
n è PARI.
Come abbiamo già avuto modo di dire anche nella precedente lezione è necessario che il RADICANDO sia POSITIVO o UGUALE A ZERO affinché sia possibile estrarre la sua radice. Quindi sarà necessario che:

A questo punto dovremmo andare ad elevare entrambi i membri all'ennesima potenza:
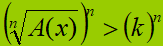
che equivale a risolvere la disequazione:
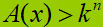
Infine dovremmo andare a trovare le soluzioni che soddisfano entrambe le disequazioni.
Osserviamo però che, se
- se k
< 0, affinché la disequazione
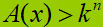
sia verificata è sufficiente porre la condizione

poiché un valore positivo è sempre maggiore di uno negativo. Quindi, per risolvere questo tipo di disequazione è sufficiente risolvere

- se k
> 0, osserviamo che, nel momento in cui
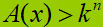
poiché
k > 0
sarà anche vero che A(x)è maggiore di zero, o uguale ad esso. Quindi, per risolvere questo tipo di disequazione è sufficiente risolvere la disequazione:
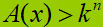
Esempio 1:
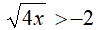
In questo caso n è pari (n = 2) e k è negativo (k = -2). Quindi andiamo a porre solamente la condizione che il radicando sia maggiore o uguale a zero. Ovvero:
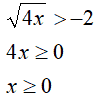
Esempio 2:
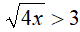
In questo caso n è pari (n = 2) e k è positivo (k = 3), quindi è sufficiente elevare al quadrato entrambi i membri della disequazione:
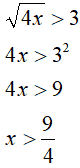
Anche in questo caso andiamo a vedere cosa accade se invece del segno > avessimo il segno ≥?
Come abbiamo detto nella lezione precedente sarà sufficiente sostituire al simbolo > quello di ≥ .
Esempio:
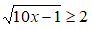
In questo caso compare il simbolo ≥. Trattandosi di una disequazione con n pari (n = 2) e k positivo ((k = 2) sarà sufficiente elevare entrambi i membri al quadrato: