DISEQUAZIONI IRRAZIONALI FRATTE
In questa lezione ci occuperemo delle DISEQUAZIONI IRRAZIONALI FRATTE. Cioè di disequazioni nelle quali:
- l'INCOGNITA si trova sotto il segno di RADICE (disequazione irrazionale);
- l'INCOGNITA si trova a DENOMINATORE di una frazione (disequazione fratta).
Alcuni esempi di questo tipo di disequazioni sono:
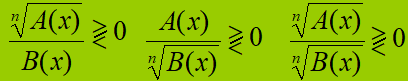
Ovviamente, le disequazioni irrazionali fratte potranno assumere anche un aspetto più complesso, ma di questo parleremo più avanti. Ora ci soffermeremo sulle disequazioni irrazionali fratte che hanno una forma riconducibile ad una di quelle appena esposte. Notiamo che, in tutti e tre i casi, a SECONDO MEMBRO abbiamo lo ZERO.
Nel risolvere questo tipo di disequazioni dobbiamo sempre ricordare che:
- se ci sono dei radicali con INDICE PARI, occorre porre la condizione che i relativi RADICANDI siamo MAGGIORI o UGUALI a ZERO. Ricordiamo che se l'indice dei radicali è dispari non c'è bisogno di porre alcuna condizione;
- altra condizione è che il DENOMINATORE della FRAZIONE sia diverso da zero;
- infine si va a STUDIARE il SEGNO della FRAZIONE.
Vediamo alcuni esempi.
1° esempio:
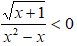
La disequazione contiene un radicale al numeratore, l'incognita a denominatore, mentre al secondo membro abbiamo solo lo zero.
Prima osservazione. Il radicale presente a numeratore è di indice pari. Quindi la prima condizione da porre è che il radicando sia maggiore o uguale a zero. Ovvero:
x + 1 ≥ 0.
La seconda condizione da porre è che il denominatore sia diverso da zero:
x2 - x ≠ 0.
Poste queste condizioni possiamo studiare il segno della frazione.
Questo significa risolvere il seguente sistema:
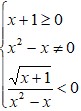
Risolviamo la prima disequazione:
x ≥ - 1.
Risolviamo la seconda disequazione:
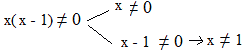
Passiamo all'ultima disequazione:
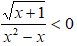
Numeratore:
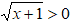
che equivale a risolvere
x + 1 > 0
x > - 1
Denominatore: x2 - x > 0
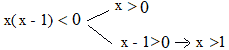
x < 0
x > 1
Segno della frazione:
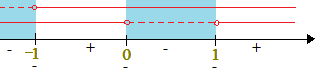
Soluzione della disequazione:
x ≤ - 1
0 ≤ x ≤ 1.
Quindi, sostituendo le soluzioni al nostro sistema, esso diventa:
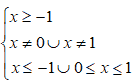
Le soluzioni del sistema sono:
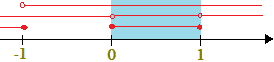
La soluzione della disequazione è data dalle
0 < x < 1.
Il modo di procedere nella risoluzione delle disequazioni irrazionali fratte è lo stesso anche nel caso in cui il radicale si trova a denominatore o il radicale si trova sia a numeratore che a denominatore.
E se a secondo membro non abbiamo lo zero?
Dopo aver posto le condizioni relative:
- ai RADICALI DI INDICE PARI, i cui radicandi devono essere maggiori o uguali a zero;
- e al DENOMINATORE, che deve essere diverso da zero;
bisogna ELEVARE primo e secondo membro all'INDICE del radicale. Quindi si porta il secondo membro a primo, cambiandogli di segno e si procede con i conteggi.
Vediamo un esempio:
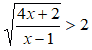
Il sistema da risolvere sarà:
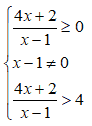
Prima disequazione:
Numeratore: 4x+2 ≥ 0 --> 4 x ≥-2 --> x≥-2/4 --> x ≥-1/2
Denominatore: x-1 >0 --> x > 1
Segno della frazione:
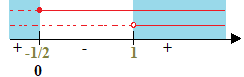
soluzione
x ≤ -1/2
x > 1.
Seconda disequazione:
x - 1 ≠ 0 ≥ --> x ≠1.
Terza disequazione:
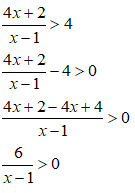
Il numeratore è un numero positivo quindi la frazione sarà positiva solamente quando anche il denominatore è positivo. Ovvero quando:
x - 1 > 0
x > 1.
Soluzione del sistema:
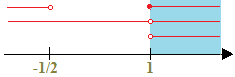
x > 1.






