PRIMO TEOREMA DI LAPLACE
- Matrice
- Matrice quadrata
- Determinante di una matrice quadrata
- Calcolo del determinante di una matrice di ordine 1
- Calcolo del determinante di una matrice di ordine 2
- Calcolo del determinante di una matrice di ordine 3
- Minore complementare
- Complemento algebrico
Nelle lezioni precedenti abbiamo visto come è possibile calcolare il DETERMINANTE di una MATRICE QUADRATA di primo, di secondo e di terzo ordine.
In questa lezione vedremo una regola che ci permetterà di calcolare il DETERMINANTE di una MATRICE QUADRATA di ordine n con
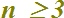
che si legge
n maggiore uguale a tre.
Quindi, la regola che vedremo, ci permetterà di trovare il determinante di una matrice quadrata di ordine UGUALE o SUPERIORE a 3.
Il DETERMINANTE associato alla matrice quadrata A si può calcolare come SOMMA dei PRODOTTI degli ELEMENTI di una RIGA o di una COLONNA per i RISPETTIVI COMPLEMENTI ALGEBRICI.
Esempio.
Consideriamo la matrice A di ordine 3:
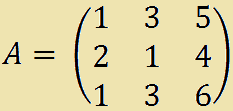
Ora scegliamo una riga o una colonna della matrice a nostro piacere: scegliamo, ad esempio, la seconda riga.
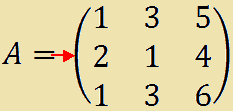
Ora calcoliamo il prodotto degli elementi della seconda riga per i rispettivi complementi algebrici e li sommiamo tra loro.
Avremo:
- iniziamo dal primo elemento della seconda riga, 2. Seconda riga, prima colonna, quindi si tratta dell'elemento a21;
- calcoliamo il prodotto di tale elemento per il suo complemento algebrico
2 · (-1)2+1· M21
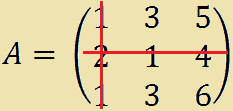
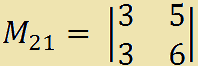
2 · (-1)2+1 · (3·6 - 5·3) =
= 2 · (-1)3 · (18 - 15) =
= 2 · (-1)· 3 =
= -6.
- Ora passiamo al secondo elemento della seconda riga, 1. Seconda riga, seconda colonna, quindi si tratta dell'elemento a22;
- calcoliamo
il prodotto di tale elemento per il suo complemento algebrico
1 · (-1)2+2 · M22
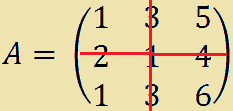
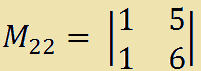
1 · (-1)2+2 · (1·6 - 5·1) =
= 1 · (-1)4 · (6 - 5) =
= 1 · 1 · 1 =
= 1.
- Continuiamo con l'ultimo elemento della seconda riga 4. Seconda riga, terza colonna, quindi si tratta dell'elemento a23;
- calcoliamo
il prodotto di tale elemento per il suo complemento algebrico
4 · (-1)2+3 · M23
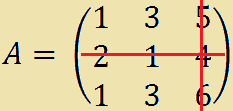
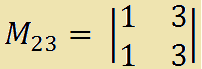
4 · (-1)2+3 · (1·3 - 3·1) =
= 4 · (-1)5 · (3 - 3) =
= 4 · (-1) · 0 =
= 0.
Ora sommiamo i tre valori ottenuti ed avremo:
-6 + 1 + 0 = -5.
Il determinante della nostra matrice è -5.
La regola che abbiamo appena illustrata prende il nome di PRIMO TEOREMA DI LAPLACE.
Nella prossima lezione vedremo un altro esempio di applicazione del primo teorema di Laplace.






