PRIMO TEOREMA DI LAPLACE: ESEMPIO DI CALCOLO DI UN DETERMINANTE
- Matrice
- Matrice quadrata
- Determinante di una matrice quadrata
- Calcolo del determinante di una matrice di ordine 1
- Calcolo del determinante di una matrice di ordine 2
- Calcolo del determinante di una matrice di ordine 3
- Minore complementare
- Complemento algebrico
- Primo teorema di Laplace
Nella lezione precedente abbiamo visto in cosa consiste il PRIMO TEOREMA DI LAPLACE e come applicarlo per calcolare il DETERMINANTE di una matrice quadrata di ordine uguale o superiore a 3.
Ora, per rendere più chiari i concetti appresi, faremo un ulteriore esempio.
Esempio.
Vogliamo calcolare il determinante della matrice A:
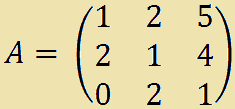
Iniziamo con lo scegliere una riga o una colonna qualsiasi della matrice. Ad esempio scegliamo la prima colonna.
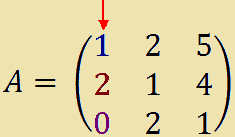
Il PRIMO TEOREMA DI LAPLACE ci dice che il DETERMINANTE associato alla matrice quadrata A si può calcolare come SOMMA dei PRODOTTI degli ELEMENTI di una RIGA o di una COLONNA per i RISPETTIVI COMPLEMENTI ALGEBRICI.
Procediamo allora con il calcolo.
det A = 1 · (-1)1+1 · M11+2 · (-1)2+1 · M21+ · (-1)3+1 · M31.
Calcoliamo i complementi algebrici ed avremo:
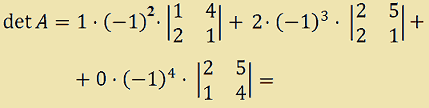
= 1 · 1 · [(1·1) - (4·2)] + 2 · (-1) · [(2·1) - (5·2)] + 0 · 1 · [(2·4) - (5·1)] =
= 1· 1 · (-7) + 2 · (-1) · (-8) + 0 · 1 · 3 =
= -7 + 16 + 0 = +9.
Il determinante della nostra matrice è 9.






