MATRICE AGGIUNTA
- Matrice
- Matrice quadrata
- Matrici trasposte
- Sottomatrice
- Minore complementare
- Complemento algebrico
- Determinante di una matrice quadrata
Data una MATRICE QUADRATA A di ordine n, chiamiamo MATRICE AGGIUNTA di A, la matrice i cui elementi sono i COMPLEMENTI ALGEBRICI dei CORRISPONDENTI elementi della TRASPOSTA di A.
La MATRICE AGGIUNTA di A si indica con
agg A
o
agg (A).
Esempio.
Consideriamo la matrice quadrata A di ordine 3:

Ora troviamo la MATRICE TRASPOSTA di A, che si indica con AT. Ricordiamo che la matrice trasposta di una matrice data si ottiene SCAMBIAMO tra loro ordinatamente le RIGHE con le COLONNE. Quindi:
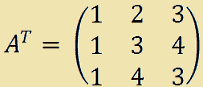
Ora dobbiamo trovare la MATRICE AGGIUNTA, cioè la matrice che ha per elementi i COMPLEMENTI ALGEBRICI dei corrispondenti elementi di AT.
Ricordiamo che:
- il COMPLEMENTO
ALGEBRICO dell'elemento aij
è il PRODOTTO del suo MINORE
COMPLEMENTARE per (-1)i+j,
ovvero:
(-1)i+j · Mij;
- il MINORE COMPLEMENTARE di un suo elemento aij, è il DETERMINANTE della SOTTOMATRICE che si ottiene da A eliminando la riga i-esima e la colonna j-esima.
Partiamo allora dalla matrice trasposta e iniziamo a vedere quale sarà l'elemento della prima riga e della prima colonna della matrice aggiunta.

L'elemento della prima riga e della prima colonna della MATRICE AGGIUNTA sarà dato dal complemento algebrico dell'elemento 1, cioè dal prodotto di (-1)i+j per il suo minore complementare che si ottiene calcolando il determinante della sottomatrice ottenuta da AT eliminando la prima riga e la prima colonna.
Ovvero:
(-1)1+1 · M11
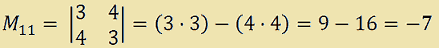
(-1)2 · (-7) = +1 · (-7) = -7.
L'elemento della prima riga e della prima colonna della MATRICE AGGIUNTA sarà -7.
Quindi possiamo dire che la matrice aggiunta sarà:

Ovvero:
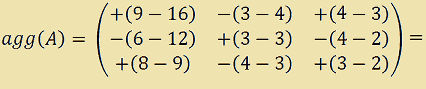

Abbiamo così calcolato la MATRICE AGGIUNTA di A.






