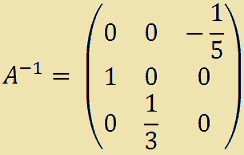CALCOLO DELLA MATRICE INVERSA
- Matrice
- Matrice quadrata
- Matrice identità
- Matrici inverse
- Matrici equivalenti
- Matrice di forma canonica
- Riduzione a forma canonica di una matrice
- Riduzione a forma canonica di una matrice
- Esistenza e calcolo delle matrici inverse
Nella lezione precedente abbiamo visto che, data una matrice quadrata A, essa ammette la MATRICE INVERSA se il suo determinante è diverso da zero.
Abbiamo anche visto un primo metodo di calcolo della matrice inversa che consiste nel dividere, ogni elemento dell'aggiunta di A, per il determinante di A.
Ora vedremo un procedimento di calcolo della MATRICE INVERSA molto più semplice e veloce che prende il nome di METODO di GAUSS-JORDAN.
Per calcolare la MATRICE INVERSA della MATRICE QUADRATA A di ordine n occorre:
- AFFIANCARE alla matrice A la MATRICE IDENTITA' di UGUALE ORDINE. In questo modo si otterrà una matrice di ordine n x 2n;
- APPLICARE sulla matrice così ottenuta le OPERAZIONI ELEMENTARI necessarie a ridurre la matrice A a FORMA CANONICA;
- la MATRICE UNITA' affiancata sarà stata TRASFORMATA nella matrice A-1.
Vediamo come applicare il metodo di Gauss-Jordan con un esempio.
Esempio.
Consideriamo la matrice
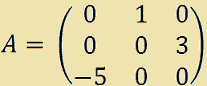
La nostra matrice ha ordine 3. Quindi affianchiamo alla matrice A la matrice identità di ordine 3. Otterremo così una matrice di ordine 3x6:
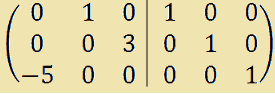
In alcuni testi le due matrici, la matrice A e la matriceI, non sono separate dalla linea verticale. Quindi la nuova matrice viene scritta così:
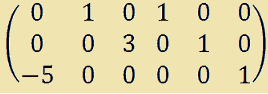
Noi opteremo per la prima soluzione che ci sembra più chiara.
Ora applichiamo le operazioni elementari in modo tale che la matrice A venga trasformata in una matrice identità:

La matrice identità, così come risulta dopo le trasformazioni eseguite, rappresenta la matrice inversa di A:

Quindi: