PARABOLA CON VERTICE NELL'ORIGINE DEGLI ASSI: ALCUNI ESEMPI
Nella lezione precedente abbiamo visto che l'equazione
y = ax2
con
a ≠ 0
è l'equazione di una PARABOLA che ha come VERTICE l'ORIGINE DEGLI ASSI e come ASSE DI SIMMETRIA l'ASSE DELLE y.
Ora supponiamo di voler disegnare l'equazione delle seguenti parabole:
- y = x2;
- y = 2x2;
- y = 3x2.
In tutti e tre i casi
a > 0
quindi, in tutti e tre i casi la parabola ha la CONCAVITA' rivolta verso l'ALTO.
Ecco i grafici delle tre equazioni:

Le tre parabole disegnate presentano un'apertura via via inferiore all'aumentare del valore di a. Potremmo anche dire che l'apertura della parabola si riduce all'aumentare del VALORE ASSOLUTO di a.
Infatti:
| 1 | = 1
| 2 | = 2
| 3 | = 3.
Ora vogliamo disegnare l'equazione delle seguenti parabole:
- y = -x2;
- y = -2x2;
- y = -3x2.
In tutti e tre i casi
a < 0
quindi, in tutti e tre i casi la parabola ha la CONCAVITA' rivolta verso il BASSO.
Ecco i grafici delle tre equazioni:
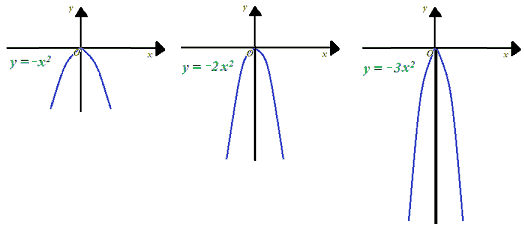
Le tre parabole disegnate presentano un'apertura via via inferiore man mano che il valore di a diminuisce. Potremmo anche dire che l'apertura della parabola si riduce all'aumentare del VALORE ASSOLUTO di a.
| -1 | = 1
| -2 | = 2
| -3 | = 3.
Quindi, come regola generale (cioè a prescindere dal fatto che a abbia segno positivo o negativo) possiamo dire che l'apertura della parabola si riduce all'aumentare del VALORE ASSOLUTO di a.
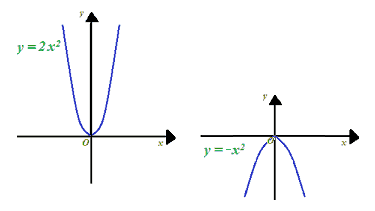
Così, ad esempio, se confrontiamo le due parabole:
- y = 2x2;
- y = -x2
notiamo che il valore assoluto di a è uguale:
- nella prima funzione a 2;
- nella seconda funzione a 1.
Quindi, poiché l'apertura della parabola si riduce all'aumentare del VALORE ASSOLUTO di a, possiamo dire che la prima parabola ha un'apertura inferiore rispetto alla seconda.
Il grafico che segue conferma quanto detto: