TEOREMA DI PITAGORA E TRIANGOLO ISOSCELE
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Le formule inverse del teorema di Pitagora
- Triangolo isoscele
- Triangolo rettangolo
- Poligoni equiangoli poligoni equilateri poligoni regolari
- Perimetro di un poligono
Disegniamo un TRIANGOLO ISOSCELE ABC:

Nella figura sopra abbiamo indicato con l il lato obliquo del triangolo. Ricordiamo che, essendo il triangolo isoscele, i due lati obliqui sono congruenti.
Abbiamo indicato con b, invece, la base del triangolo.
Osserviamo che l'ALTEZZA h DIVIDE il nostro triangolo isoscele in due TRIANGOLI RETTANGOLI congruenti.
I due triangoli rettangoli hanno:
- come CATETI, rispettivamente, l'altezza h e metà della base b, cioè b/2;
- come IPOTENUSA il lato l.
Di conseguenza, se conosciamo l'altezza e la base del triangolo isoscele e vogliamo trovare il suo lato, potremo utilizzare il teorema di Pitagora e scrivere:

Come formule inverse avremo:
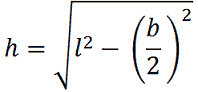

Esempio:
calcolare il perimetro di un triangolo isoscele la cui altezza misura m 4 e il cui lato obliquo misura m 6.
Noi dobbiamo calcolare il perimetro del triangolo. Per poterlo ottenere abbiamo bisogno di conoscere la misura del lato obliquo e della base del triangolo.
Noi sappiamo quanto misura il lato obliquo perciò dobbiamo trovare la misura della base.
Applichiamo la formula:

Abbiamo trovato la misura di b/2, cioè metà base. Quindi la base sarà uguale a:
b/2 = 4,47 x 2 = 8,94 m.
Ora conosciamo sia la misura della base che quella del lato obliquo e possiamo trovare il perimetro:
P = 8,94 + 6 + 6 = m 20,94.






