TEOREMA DI PITAGORA E POLIGONI CIRCOSCRITTI
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Le formule inverse del teorema di Pitagora
- Poligoni circoscritti
- Triangolo isoscele
- La circonferenza e il cerchio
- Area di un poligono circoscritto
- Perimetro di un poligono
- Area del triangolo
In questa lezione vogliamo vedere le possibili applicazioni del TEOREMA DI PITAGORA al caso di un POLIGONO CIRCOSCRITTO AD UNA CIRCONFERENZA: lo faremo attraverso un esempio.
Esempio:
un triangolo isoscele ha la base lunga cm 12 e il lato obliquo lungo cm 10. Calcolare il raggio della circonferenza inscritta nel triangolo.
Iniziamo col disegnare il triangolo isoscele e la circonferenza inscritta in essa:
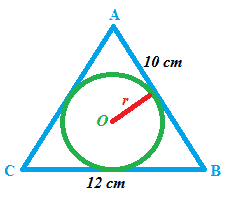
Per risolvere un problema di questo tipo dobbiamo ricordare l'AREA di un POLIGONO CIRCOSCRITTO ad un cerchio è uguale al SEMIPRODOTTO della misura del PERIMETRO della figura per il RAGGIO. Ovvero:
A = (P x r)/ 2
dove
A = area del poligono
P = perimetro del poligono
r = raggio.
Da questa formula si ottiene quella per determinare il raggio, ovvero:
r = (2 x A)/ P.
Quindi, se troviamo il perimetro e l'area del triangolo, possiamo trovare il raggio.
Il perimetro del triangolo possiamo calcolarlo, dato che sappiamo la misura di tutti i suoi lati. Avremo:
P = 12 + 10 + 10 = cm 32.
Per trovare l'area del triangolo dobbiamo calcolare la sua altezza: possiamo farlo applicando il teorema di Pitagora:
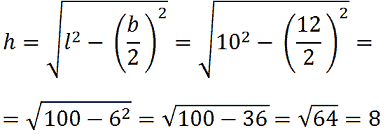
Ora sappiamo che l'altezza misura cm 8 possiamo trovare l'area del triangolo:
A = (b x h)/ 2
A = (12 x 8) / 2 = cm2 48.
Ora abbiamo tutti i dati per poter risolvere il problema. Basterà applicare la formula precedente:
r = (2 x A)/ P = (2 x 48)/ 32 = 96/ 32 = 3 cm.
Abbiamo trovato la misura del raggio: 3 cm.






