RAZIONALIZZAZIONE DEL DENOMINATORE DI UNA FRAZIONE
- Radicali quadratici
- Radicali di indice n
- Prima proprietà fondamentale dei radicali
- Le frazioni
- Frazioni equivalenti
- Somma algebrica di numeri relativi
- Somma di due monomi per la loro differenza
- Prima proprietà fondamentale dei radicali
Può accadere, quando si risolvono delle espressioni, di trovarsi di fronte a delle FRAZIONI al cui DENOMINATORE compaiono dei RADICALI.
Esempio:

In questo caso, per semplificare i calcoli, è opportuno TRASFORMARE la frazione data in una FRAZIONE EQUIVALENTE priva di radicali al denominatore.
Questa operazione prende il nome di RAZIONALIZZAZIONE DEL DENOMINATORE di una frazione.
Come bisogna procedere?
Si tratta di MOLTIPLICARE NUMERATORE e DENOMINATORE della frazione per uno STESSO FATTORE, scelto opportunamente, in modo da consentirci di eliminare il radicale presente al denominatore.
Per la PROPRIETA' INVARIANTIVA delle frazioni, così facendo, trasformiamo la frazione data in una frazione equivalente.
Il fattore per il quale moltiplichiamo numeratore e denominatore della frazione prende il nome di FATTORE RAZIONALIZZANTE.
Di seguito vedremo alcuni esempi per capire come scegliere il fattore razionalizzante.
1° CASO: frazione con, a denominatore, un RADICALE QUADRATICO
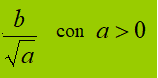
In questo caso il FATTORE RAZIONALIZZANTE è il DENOMINATORE della frazione. Infatti, se moltiplichiamo numeratore e denominatore per la radice quadrata di a e, successivamente, applichiamo la prima proprietà fondamentale dei radicali, avremo:

Abbiamo così ottenuto una frazione equivalente a quella data che non ha nessun radicale a denominatore.
Esempi:

2° CASO: frazione con, a denominatore, un RADICALE DI INDICE n

Ora ipotizziamo che
m < n
In questo caso il FATTORE RAZIONALIZZANTE è

Infatti:

Esempi:

Se, invece
m > n
bisogna PORTARE FUORI il fattore a con un adeguato esponente e successivamente procedere alla razionalizzazione.

3° CASO: frazione con, a denominatore, la SOMMA ALGEBRICA di DUE RADICALI QUADRATICI

In questo caso il FATTORE RAZIONALIZZANTE è

Infatti:

A denominatore applichiamo la regola della somma di due monomi per la loro differenza e, successivamente, la prima proprietà fondamentale dei radicali e avremo:

Esempio:

Se, invece:

In questo caso il FATTORE RAZIONALIZZANTE è

Omettiamo la dimostrazione che è del tutto simile a quella vista in precedenza.
4° CASO: frazione con, a denominatore, la SOMMA ALGEBRICA di un RADICALE QUADRATICO e un NUMERO RAZIONALE

In questo caso il FATTORE RAZIONALIZZANTE è
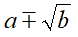
In altre parole, in maniera simile a quanto visto nel caso precedente:
- se a denominatore della frazione c'è una SOMMA il fattore razionalizzante è una DIFFERENZA;
-
se a denominatore della frazione c'è una DIFFERENZA il fattore razionalizzante è una SOMMA.
Dimostriamo, quanto abbiamo detto, considerando l'ipotesi che a denominatore vi sia la somma di un radicale quadratico e di un numero razionale. Ovviamente, la dimostrazione sarà analoga per il caso della differenza.

Esempio:

Ovviamente, la regola vale anche se la frazione si presenta nel modo seguente:

Chiaramente, in questo caso il FATTORE RAZIONALIZZANTE sarà







