RELAZIONI TRIGONOMETRICHE PER UN TRIANGOLO RETTANGOLO
Dopo aver accennato a cos'è la trigonometria e quali sono state le sue origini, entriamo nel vivo dell'argomento occupandoci delle RELAZIONI TRIGONOMETRICHE PER UN TRIANGOLO RETTANGOLO.
Disegniamo un triangolo rettangolo:
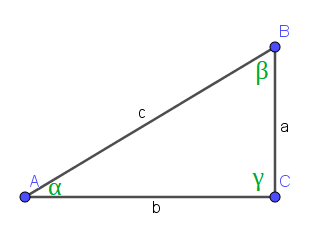
Nell'immagine sopra abbiamo chiamato:
- con α la misura dell'angolo Â;
- con β la misura dell'angolo B̂;
- con γ la misura dell'angolo Ĉ;
- con a la misura del lato BC opposto al vertice A;
- con b la misura del lato AC opposto al vertice B;
- con c la misura del lato AB opposto al vertice C;
Ora disegniamo una circonferenza goniometrica che abbia centro in A:
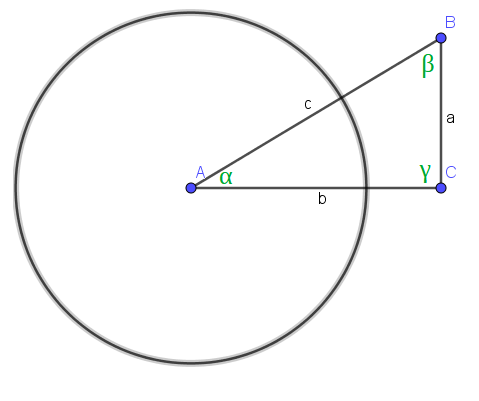
Ora indichiamo con P il PUNTO IN CUI IL LATO AB INCONTRA LA CIRCONFERENZA GONIOMETRICA:
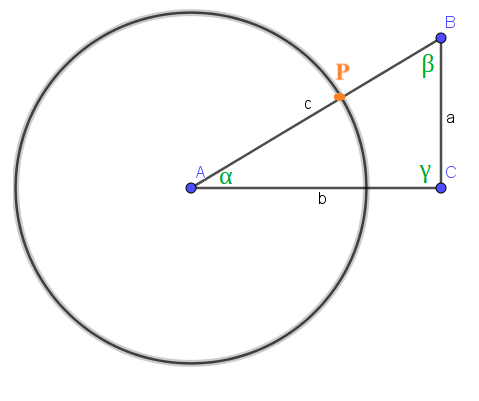
e disegniamo il punto H che rappresenta la PROIEZIONE DEL PUNTO P SUL LATO AC.
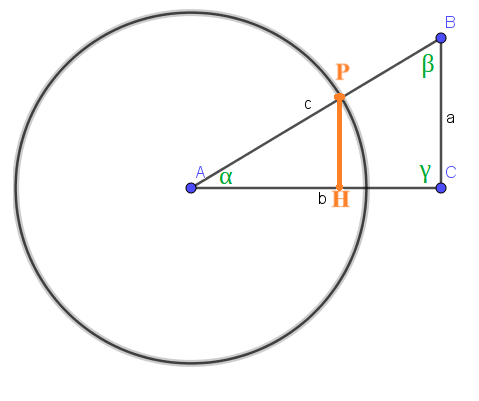
Osserviamo che i TRIANGOLI APH e ABC SONO SIMILI.
Di conseguenza possiamo dire che:
BC : AB = PH : AP
e anche che
AC : AB = AH : AP
Ora noi sappiamo che:
- il SEGMENTO AP è pari a 1;
- il SEGMENTO PH non è altro che il sen α;
- il SEGMENTO AH non è altro che il cos α.
Quindi:
BC : AB = PH : AP
diventa
BC : AB = sen α : 1
da cui otteniamo che:
BC = (AB · sen α)/ 1
ovvero
BC = AB · sen α
Ma poiché BC non è altro che il lato del triangolo che abbiamo chiamato a e AB è il lato del triangolo che abbiamo chiamato c possiamo scrivere la nostra formula anche nel modo che segue:
a = c · sen α.
La seconda proporzione da noi scritta è:
AC : AB = AH : AP
che diventa
AC : AB = cos α : 1
da cui otteniamo che:
AC = (AB · cos α)/ 1
ovvero
AC = AB · cos α
Ma poiché AC non è altro che il lato del triangolo che abbiamo chiamato b e AB è il lato del triangolo che abbiamo chiamato c possiamo scrivere la nostra formula anche nel modo che segue:
b = c · cos α.
Queste due eguaglianze ci permettono di formulare il PRIMO TEOREMA DEI TRIANGOLI RETTANGOLI. Esso afferma che:
IN UN TRIANGOLO RETTANGOLO LA MISURA DI UN CATETO E' UGUALE A QUELLA DELL'IPOTENUSA MOLTIPLICATA PER IL SENO DELL'ANGOLO OPPOSTO AL CATETO O PER IL COSENO DELL'ANGOLO ACUTO ADIACENTE AL CATETO.
In altre parole:
CATETO = IPOTENUSA · SENO DELL'ANGOLO OPPOSTO
oppure
CATETO = IPOTENUSA · COSENO DELL'ANGOLO ACUTO ADIACENTE
Nella prossima lezione vedremo una seconda relazione trigonometrica per un triangolo rettangolo.






