SECONDO TEOREMA DEI TRIANGOLI RETTANGOLI
Dopo aver visto, nella lezione precedente, il PRIMO TEOREMA DEI TRIANGOLI RETTANGOLI, passiamo ora al SECONDO TEOREMA.
Riprendiamo l'immagine costruita nella lezione precedente:
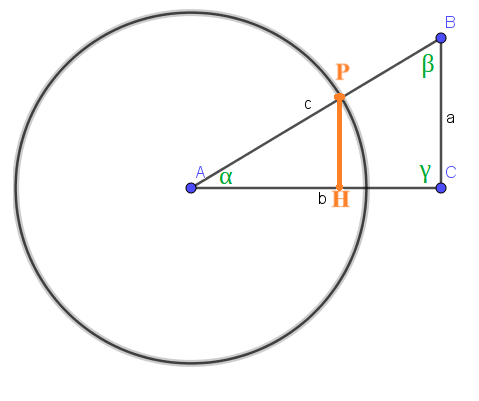
Come avevamo avuto modo di osservare, i TRIANGOLI APH e ABC SONO SIMILI.
Di conseguenza possiamo dire che:
BC : AC = PH : AH
che equivale a scrivere
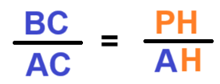
Ma poiché PH non è altro che il sen α e AH non è altro che il cos α, possiamo scrivere:
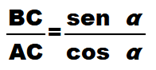
Ricordando che la TANGENTE di un angolo non è altro che il RAPPORTO tra il suo SENO e il suo COSENO avremo:
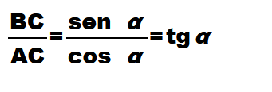
da cui, moltiplicando primo e secondo membro per AC, otteniamo:

Ma poiché BC non è altro che il lato del triangolo che abbiamo chiamato a e AC non è altro che il lato del triangolo che abbiamo chiamato b, avremo:

D'altra parte, poiché:
BC : AC = PH : AH
possiamo scrivere che
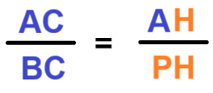
Ma, come abbiamo già detto, AH non è altro che il cos α e PH è il sen α. Quindi possiamo scrivere:
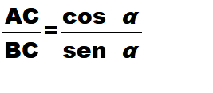
Ricordando che il RAPPORTO tra il COSENO e il SENO di un ANGOLO non è altro che la sua COTANGENTE avremo:
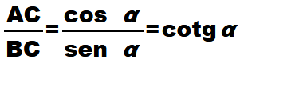
da cui, moltiplicando primo e secondo membro per BC, otteniamo:
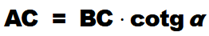
Ma poiché AC non è altro che il lato del triangolo che abbiamo chiamato b e BC non è altro che il lato del triangolo che abbiamo chiamato a, avremo:

Possiamo, quindi, formulare il SECONDO TEOREMA DEI TRIANGOLI RETTANGOLI. Esso afferma che:
IN UN TRIANGOLO RETTANGOLO LA MISURA DI UN CATETO E' UGUALE A QUELLA DELL'ALTRO CATETO MOLTIPLICATA PER LA TANGENTE DELL'ANGOLO OPPOSTO AL PRIMO CATETO O PER LA COTANGENTE DELL'ANGOLO ACUTO ADIACENTE AL PRIMO CATETO.
In altre parole:
CATETO = ALTRO CATETO · TANGENTE DELL'ANGOLO OPPOSTO AL PRIMO CATETO
oppure
CATETO = ALTRO CATETO · COTANGENTE DELL'ANGOLO ACUTO ADIACENTE AL PRIMO CATETO






