RISOLUZIONE DEI TRIANGOLI RETTANGOLI
Ora che sappiamo cosa affermano il PRIMO e il SECONDO TEOREMA DEI TRIANGOLI RETTANGOLI vediamo cosa significa RISOLVERE UN TRIANGOLO RETTANGOLO.
Con questa espressione si intende che andiamo a DETERMINARE le MISURE dei suoi LATI e dei suoi ANGOLI. Affinchè ciò sia possibile è NECESSARIO CONOSCERE ALMENO UN LATO e UN ALTRO DEI SUOI ELEMENTI.
Se di un triangolo conosciamo solamente gli angoli, non saremo in grado di determinare i lati, poichè esistono infiniti
triangoli, tutti simili al dato, che hanno gli angoli congruenti.
Nella RISOLUZIONE DEI TRIANGOLI RETTANGOLI si potranno avere 4 CASI DIVERSI:
- conosciamo due lati che possono essere:
- DUE CATETI;
- UN CATETO E L'IPOTENUSA;
- conosciamo un lato e un angolo che possono essere:
- UN CATETO e UN ANGOLO ACUTO;
- L'IPOTENUSA e UN ANGOLO ACUTO.
Iniziamo a vedere, in questa lezione, un esempio pratico relativo all'ipotesi in cui SONO NOTE LE MISURE DEI DUE CATETI.
Esempio:
Dato il triangolo rettangolo ABC, rettangolo in A, e sapendo che b = 12 e c = 5 risolvere il triangolo.
I dati di partenza sono:
- b = 12 che è la lunghezza di un cateto
- c = 5 che è la lunghezza dell'altro cateto.
Chiamiamo:
AB = b
AC = c
BC = a.
Inoltre poniamo:
l'angolo C = γ
l'angolo B = β.
Dobbiamo trovare:
- la lunghezza dell'ipotenusa a;
- gli angoli B e C ovvero i due angoli acuti del triangolo.
Iniziamo col disegnare il triangolo:
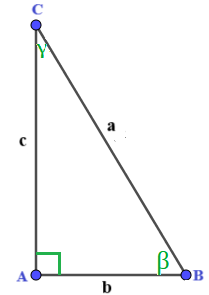
In questo caso sono NOTI DUE CATETI.
Quindi, per prima cosa, possiamo trovare l'IPOTENUSA applicando il TEOREMA DI PITAGORA:
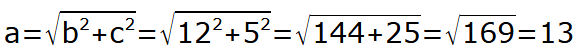
Quindi l'ipotenusa a = 13.
Ora passiamo a calcolare gli angoli β e γ.
Per farlo possiamo applicare il PRIMO TEOREMA DEI TRIANGOLI RETTANGOLI il quale ci dice che un cateto è uguale al prodotto tra l'ipotenusa e il seno dell'angolo opposto.
Nel nostro caso, quindi, possiamo scrivere:
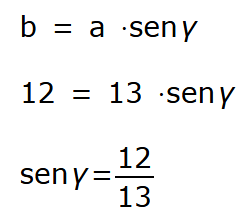
Quindi per trovare l'angolo il cui seno è pari a 12/13 ricorriamo all'ARCOSENO ed abbiamo:
A questo punto non ci resta che trovare l'altro angolo acuto. Avremo:
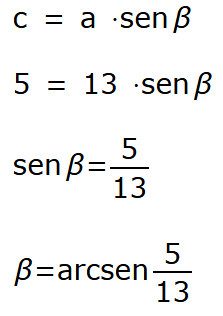
Pertanto, ricapitolando, i risultati:
LATI:
a = 13;
b = 12;
c = 5.
ANGOLI:
A = 90°;
B = arcsen 12/13;
C = arcsen 5/13.
Nella prossima lezione vedremo come si risolvono problemi appartenenti al secondo caso, ovvero quando sono noti un cateto e l'ipotenusa.
