CONVERTIRE IN GRADI CENTESIMALI GLI ANGOLI ESPRESSI IN GRADI SESSAGESIMALI E VICEVERSA

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Nozione di angolo
• Come si misura l'ampiezza di un angolo

Dopo aver visto nella lezione precedente come si può convertire in radianti l'ampiezza di un angolo espresso in gradi sessagesimali o sessadecimali, e viceversa, in questa lezione ci occuperemo della CONVERSIONE in GRADI CENTESIMALI degli angoli espressi in GRADI SESSAGESIMALI o in GRADI SESSADECIMALI e viceversa.

In altre parole vogliamo capire come fare per sapere a quanti GRADI CENTESIMALI corrisponde un angolo, ad esempio di 30° o di 70°.

Per risolvere il problema dobbiamo ricordare che 1 GRADO CENTESIMALE (che andremo ad indicare con la sigla gon) equivale alla CENTESIMA PARTE dell'ANGOLO RETTO.

Noi sappiamo che un angolo retto misura, nel sistema sessagesimale 90°: questo significa che 1 grado centesimale equivale a 90°/100 che semplificato può essere scritto come 9°/10.

Questo ci permette di scrivere la seguente proporzione:

α° : α_gon = 9°/10 : 1

Da questa proporzione, conoscendo l'ampiezza dell'angolo in gradi sessadecimali (α°), possiamo determinare l'ampiezza dell'angolo in gradi centesimali (α_gon) nel modo seguente:

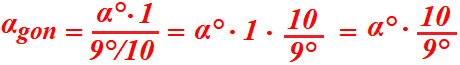
Quindi possiamo dire che:

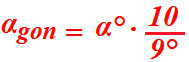
Quindi, per sapere quanti gradi centesimali misura l'angolo che nel sistema sessagesimale misura 30° basterà applicare la formula appena vista e avremo:

α_gon = α °· (10/9°) = 30° · (10/9°) = 33,33_gon

Facciamo un altro esempio: dato un angolo che nel sistema sessagesimale ha un ampiezza di 70°, vogliamo conoscere la sua ampiezza in gradi centesimali.

Andiamo ad applicare la formula vista ed avremo:

α_gon = α °· (10/9°) = 70° · (10/9°) = 77,78_gon

Così come abbiamo visto nella lezione precedente, quando abbiamo parlato di conversione dei gradi in radianti, anche in questo caso, se la misura dell'angolo espressa in gradi sessagesimali, contiene anche primi e secondi, occorrerà prima effettuare una conversione in gradi sessadecimali. Facciamo un esempio:

Esempio: vogliamo sapere la misura gradi centesimali di un angolo di 60° 20' 15''.

Innanzittutto dobbiamo convertire i gradi sessagesimali in gradi sessadecimali. Avremo:

60° 20' 15'' = 60 + (20/60)° + (15/3.600)° = 60° + 0,33333° + 0,00417° = 60,3375°.

Ora possiamo convertire i gradi sessadecimali in gradi centesimali:

α_gon = α °· (10/9°) = 60,3375° · (10/9°) = 67,04117_gon

Chiaramente la stessa proporzione ci permetterà di convertire i gradi centesimali in gradi sessadecimali. Infatti

α° : α_gon = 9°/10 : 1

Da essa otteniamo:

Quindi la formula da applicare è:

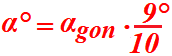
Vediamo, attraverso un esempio, come applicare la formula. Supponiamo di avere un angolo che misura 40,08_gon e vogliamo conoscere la sua ampiezza in gradi sessagesimali.

Basterà eseguire i seguenti calcoli:

α° = α_gon · 9°/10 = 40,08_gon · 9°/10 = 36,072°

In questo caso ci veniva chiesto di convertire i gradi centesimali in gradi sessadecimali. Se, invece, ci fosse stato chiesto di convertirli in gradi sessagesimali, a questo punto avremmo dovuto fare un'ulteriore conversione, ovvero:

36,072° = 36° + (0,072 · 60)° = 4,32'

36,072° = 36° + 4' + (0,32 · 60)° = 19'' (chiaramente arrotondiamo il risultato).

Quindi il risultato cercato è:

36° 4' 19''

Nella prossima lezione vedremo come convertire i gradi centesimali in radianti e viceversa.

Lezione precedente - Lezione successiva

Indice degli argomenti sugli angoli e la loro misura

Pubblicità/Advertising