GRAFICO DELLA FUNZIONE TANGENTE
Dopo aver visto cosa si intende per TANGENTE di un angolo α e come varia la tangente al variare dell'angolo α, in questa lezione andremo a vedere come possiamo rappresentare graficamente la funzione tangente, ovvero la funzione
y = tan α
e quali caratteristiche ha questa funzione.
Iniziamo col vedere come disegnare la FUNZIONE TANGENTE.
Disegniamo gli assi cartesiani:
Riporteremo:
- sull'asse delle ASCISSE i valori degli ANGOLI;
- sull'asse delle ORDINATE il corrispondente valore della TANGENTE.
Così come abbiamo fatto per la rappresentazione grafica del seno e del coseno, anche in questo caso, per rendere più semplice la costruzione del nostro grafico andiamo ad affiancare agli assi cartesiani la circonferenza goniometrica:
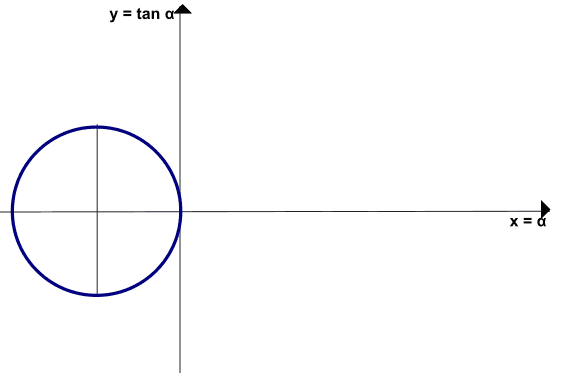
Per costruire il grafico della funzione tangente andiamo ad operare nel modo seguente:
- per ogni angolo della circonferenza goniometrica, prendiamo sull'asse delle ascisse la lunghezza del corrispondente arco;
- sulle ordinate, invece, riporteremo la lunghezza della
retta AT.
Notate che abbiamo disegnato la circonferenza goniometrica in modo tale che l'asse delle ordinate (y = tan α) sia tangente alla circonferenza goniometrica nel punto A: così facendo l'asse delle ordinate diventa automaticamente la retta AT e il punto T di interesezione tra la retta AT e la retta OP si trova proprio sull'asse delle ordinate.
Partiamo dall'angolo di ampiezza 0 radianti. Indichiamo l'angolo sugli assi cartesiani nel punto dell'origine. Quando l'angolo vale 0 radianti l'ordinata del punto T è 0. Quindi il primo punto cercato coincide con l'origine degli assi cartesiani.
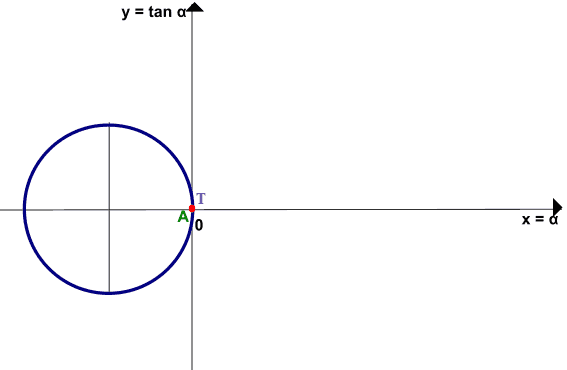
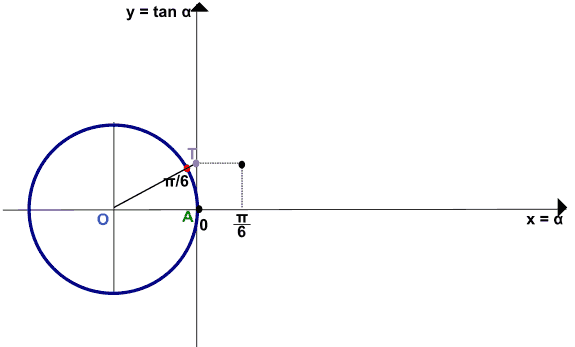
Passiamo a considerare l'angolo di ampiezza π/6: lo indichiamo sulla circonferenza goniometrica e riportiamo tale valore anche sull'ascissa degli assi cartesiani.
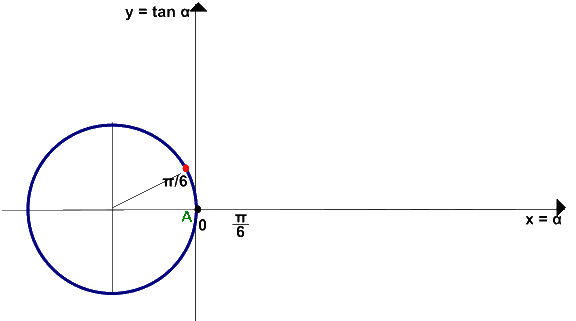
Individuiamo il punto T nel quale la retta AT, che abbiamo detto non è altro che l'asse delle ordinate, interseca la retta OP. Abbiamo individuato un secondo punto del nostro grafico.
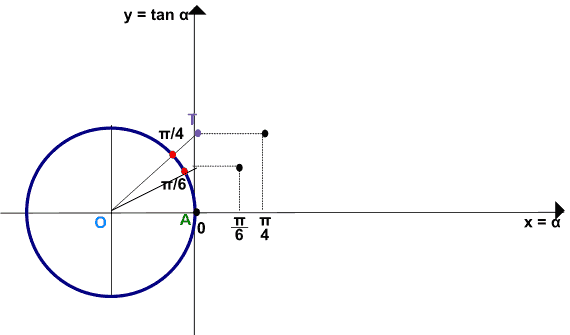
Passiamo a segnare sulla circonferenza gonomiometrica l'angolo di ampiezza π/4: riportiamo tale valore anche sull'ascissa degli assi cartesiani ed andiamo ad individuare il punto T nel quale l'asse delle ordinate, interseca la retta OP. Abbiamo trovato un altro punto del nostro grafico.
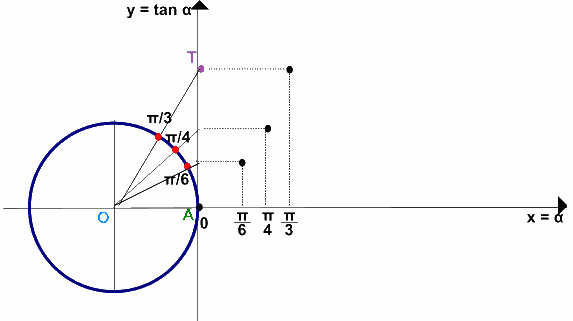
Proseguiamo indicando sulla circonferenza gonomiometrica l'angolo di ampiezza π/3 e riportiamo tale valore anche sull'ascissa degli assi cartesiani ed andiamo ad individuare il punto T nel quale l'asse delle ordinate, interseca la retta OP in modo da individuare un altro punto del nostro grafico.
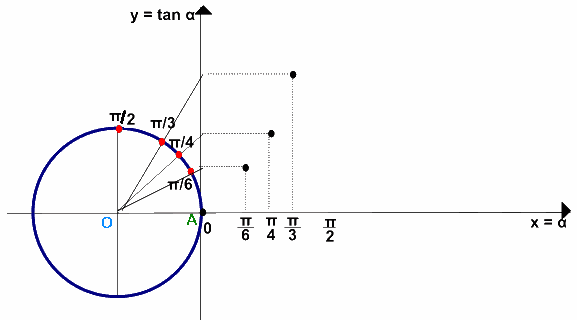
Arriviamo al valore di π/2 che segniamo sulla circonferenza goniometrica e riportiamo anche sull'ascissa degli assi cartesiani. In questo caso la retta OP è parallela all'asse delle y quindi non possiamo individuare un punto T sull'asse delle ordinate.
Proseguiamo nel costruire il grafico della funzione tangente con altri angoli della circonferenza goniometrica. Infine colleghiamo con una linea i punti individuati.
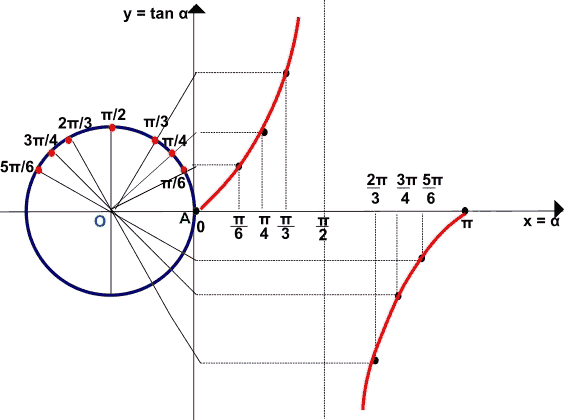
Quello che abbiamo disegnato è il GRAFICO della FUNZIONE TANGENTE: in modo particolare si tratta della porzione del grafico della funzione tangente per α compreso tra 0° e 180°.
Ora vediamo quali sono le caratteristiche di questa funzione.
Il grafico della tangente ha una forma che prende il nome di TANGENTOIDE.
La funzione, all'origine degli assi, vale zero dato che la tangente dell'angolo di ampiezza zero è zero.
Quando l'angolo α ha un'ampiezza di π/2 la funzione tangente NON è DEFINITA. Ma vediamo cosa accade intorno al punto π/2:
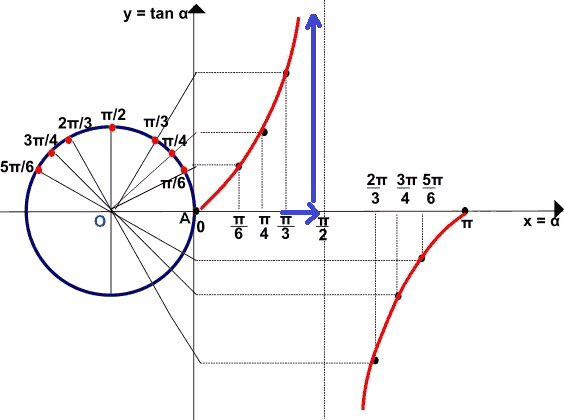
- per valori inferiori a π/2, mano a mano che l'angolo si avvicina sempre più a questo valore, la tangente tende a diventare sempre più grande.
Per questo diciamo che essa tende a
+∞ (che si legge più infinito);
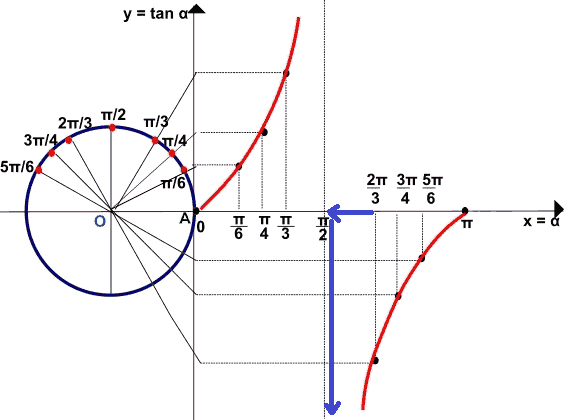
- per valori superiori a π/2 mano a mano che l'angolo si avvicina sempre più a questo valore la tangente tende a diventare sempre più piccola. Per questo diciamo che essa tende a
-∞ (che si legge meno infinito).
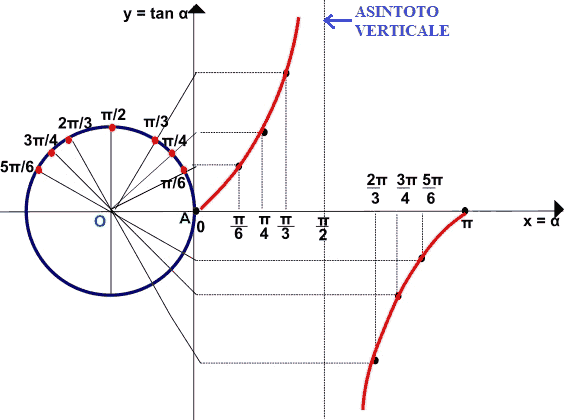
Quando il valore dell'angolo α si avvicina a π/2 la tangente si avvicina sempre più alla retta parallela all'asse delle y di equazione
x = π/2
che prende il nome di ASINTOTO VERTICALE del grafico.
Come abbiamo già avuto modo di dire nella lezione precedente la funzione tangente NON è LIMITATA dato che può assumere qualsiasi valore reale.
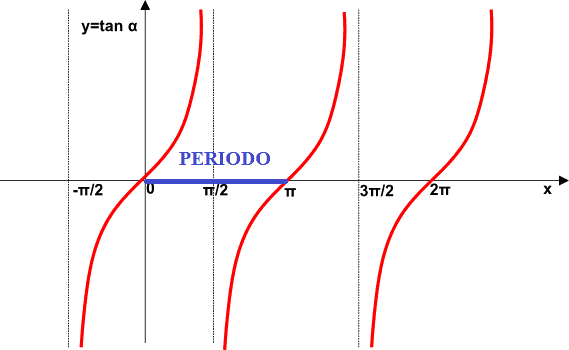
La funzione tangente è PERIODICA, esattamente come la funzione seno e quella coseno.
Il PERIODO della funzione tangente, cioè l'intervallo dopo il quale la funzione si ripete in modo identico, è π radianti.
Quando l'angolo α ha ampiezza 0 la tangente vale 0. Lo stesso valore della tangente si ha quando l'angolo vale π e ancora quando l'angolo ha ampiezza 2π e così via.
Allo stesso modo vediamo che la funzione tangente tende a +∞ quando l'angolo α si avvicina π/2 e ancora quando si avvicina 3π/2 e così via.
E potremmo continuare con altri esempi.
Quindi la funzione si ripete sempre allo stesso modo dopo un periodo di π. Infatti:
Tutto questo si scrive nel modo seguente:
tan (α + kπ) = tan α
con k appartenente all'insieme Z, cioè all' insieme dei numeri interi relativi.






